XML = Automata + Logic + Database

What do you get when you mix automata theory, mathematical logic, and database theory in a big bowl, and stir it vigorously? The answer is foundations of XML. In the past 7 - 8 years, the study of XML has generated a large number of elegant and unexpected connections between the three aforementioned areas. How so? Answer: we can view XML documents as labeled unranked trees, and we have numerous formalisms in (tree) automata theory and mathematical logic for querying and manipulating tree-like structures.

I presume you all know a little bit about HTML. XML is just like HTML but you have to define your own tags (e.g. <tag> ... </tag>). According to W3C XML tutorial, unlike HTML, whose primary goal is to display data focusing on how it looks, XML was designed to describe data and to focus on what data is. Well, then, what can you use XML for? Primarily, for information exchange on the web. In fact, one of the greatest promises of XML is to serve as the lingua franca in information exchange. Without further ado, let's look at an example of XML documents:

<books>
    <book>
        <title>Elements of Finite Model Theory</title>
        <author>Leonid Libkin</author>
        <year>2004</year>
        <publisher>Springer</publisher>
        <rank>5/5</rank>
    </book>
    <book>
        <title>Animal Farm</title>
        <author>George Orwell</author>
        <year>2003</year>
        <publisher>Penguin Books</publisher>
    </book>
</books>

One can view this document as a labeled unranked tree:


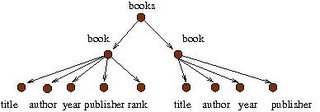
When we study foundations of XML, we care only about the structure of the tree. Consequently, we omitted the texts within the innermost tags. By definition, this tree is different from the tree that you get from exchanging the two children of "books". That is, a sibling ordering is assumed. Also, note that a node in an XML tree may have an arbitrarily large number of children. This is why the tree is said to be unranked.

We are interested in both procedural formalisms (i.e. automata) and logical formalisms (i.e. logical languages) for querying unranked trees. The intention is that we express the query in a logical language, which will then be converted to an automaton that one can run to compute the query against the XML document.

Of course, we should ask why we want to have query languages in the first place. Some answers are:

1. Validation - we wish to distinguish XML documents that make sense and those that don't. A common example arises when two parties want to exchange some information using XML documents. They of course have to agree on the formatting of the documents that they accept. Elaborating on the example above, one may insist that "books" have zero or more children with tags "book", each of which must have four children with tags (in order) "title", "author", "year", and "publisher", and one optional child with tags "rank".
   
2. Navigation. For example, one may want to ask for all nodes in the document that are tagged "book" and have a child tagged "rank".
   

For validation, the yardstick logic is monadic second-order logic (MSO). This is because MSO is essentially equivalent to XSD (XML Schema Definition) which people use for validation in practice. For navigation, the yardstick logic is first-order logic (FO). This is because FO and its fragments is closely connected to XPath, a practical XML navigational language which people use.

What kind of procedural formalisms do we have for validation and navigation? For validation, we have what we call nondeterministic unranked tree automaton (NUTA). Its connection to MSO is very tight:

Theorem: A set of unranked trees (over a fixed finite set of labels) is recognizable by a NUTA iff it is definable in MSO.

What about navigation? This is still open.

Another research direction in foundations of XML concerns finding logics, which are equivalent to the yardstick logics, whose model-checking/query evaluation is polynomial in the size of the formula and tree. It is known that both MSO and FO have horrible complexity for model-checking over trees. Research in this direction often requires one to use some kinds of modal logics. For example, we know that CTL* (Computational Tree Logic*) with past operator, which researchers in model-checking community love, is equivalent to FO over unranked trees. There are also other research directions with a plethora of interesting open problems (such as streaming XML documents). If the reader is interested, I will further elaborate on foundations of XML.