The most recent issue of SIGACT Newsletter (vol. 36, number 4) contains a guest column concerning progress in descriptive complexity by Neil Immerman. [Thanks to Kurt for making me aware of this article.] The article concisely surveys some recent progress in finite model theory with an emphasis on descriptive complexity. The style is extremely informal, and I believe is a perfect weekend read. I highly recommend the article to anybody interested in logic or computational complexity.
Let me say a little bit about the content of the article (no spoiler!). It starts by motivating the study of descriptive complexity. Then, it moves on to the spectrum problem and Fagin's theorem (that NP = existential second-order logic), which marked the beginning of descriptive complexity. We then see some other capturing results in descriptive complexity (e.g. characterizations of P, PSPACE, etc.). My favorite capturing result mentioned here is DSPACE[nv] = VAR[v+1], where VAR[k] denotes the set of problems expressible by a sequence of first-order sentences using at most k variables. And so forth ... but let me mention another interesting thing written in the article. We notice that most of the capturing results use a linear ordering on the universe. [In fact, a linear ordering is necessary for these results to work.] For example, Immerman-Vardi theorem says that FO(LFP) captures PTIME over the class of ordered structures. However, FO(LFP) does not capture PTIME over the class of all structures. In fact, a long-standing open problem in finite model theory is whether there exists a logic capturing order-independent PTIME problems. The article nicely surveys our progress towards resolving this problem. Another interesting thing that you will get to know a bit about is the phenomenon that one logic may be exponentially more "succinct" than another logic with the same expressive power.
A fair question to ask now is to what extent has descriptive complexity has helped us to answer structural complexity questions such as separating two complexity classes. Let me try to provide some answers to this question. I believe that the first switching lemma, which separates AC0 from LOGSPACE, was proved by Miklos Ajtai using finite model theory. This result was independently discovered by Saxe, Sipser, and Furst around the same time using combinatorics. Most people, even finite model theorists, think that the combinatorial proof provided by Saxe et al. is easier to understand than Ajtai's proof. [Of course, we now have Hastad's switching lemma with some elegant proofs.] Next I will mention Immerman-Szelepscenyi theorem that NSPACE(f(n)) is closed under complementation. Immerman proved this by appealing to descriptive complexity, while Szelepscenyi by using some elementary combinatorics. In this sense, a skeptic might say that descriptive complexity has not really helped structural complexity theory. But, what has? Nothing much really, with expander graphs as one only exception (recall Reingold's recently proved theorem that L = SL). On the other hand, I believe that descriptive complexity helps us understand computational complexity. Many problems or classes in complexity theory have simple and elegant correspondence in descriptive complexity theory. In fact, some logical characterizations of complexity classes are commonly used by computational complexity theorists (e.g. logical characterizations of each level in the poly-time hierarchy). In this sense, I am positive that one day somebody who understands computational complexity, with some help from descriptive complexity, will resolve some of the most tantalizing open problems in structural complexity.
Monday, December 19, 2005
Saturday, December 10, 2005
Foundations of XML: Validating XML Documents (1)
Apologies for my long silence. Things got unexpectedly hectic for me in the past two to three weeks for various reasons. Anyway, as I promised in my previous post, I will further talk about foundations of XML, should the reader be interested. I received two comments expressing interests, one from Jon Cohen, which assure me that at least somebody is going to read this post :-). So, on with our discussion on foundations of XML. Let's spend some time now talking about validation of XML documents. [I am still preparing my post on navigating XML documents and XPath.] In this post, I will talk about a practical validation language that goes by the name of DTD (Document Type Definition).
Roughly speaking, the aim of validation is to ensure that an XML document "makes sense". More precisely, the problem is that, given an XML document (i.e. a labeled unranked tree T) and a statement f in some specification language L, we want to test whether T satisfies f. The most frequently used language L for validation of XML documents is DTD (Document Type Definition). Here, we use a formal model of DTDs that does not incorporate XML "data values", e.g., texts within XML tags (see my previous post). Let us start with an example. As always, we fix a finite alphabet Σ of discourse. Continuing with our example in the previous post, suppose we want to test whether an unranked tree T satisfies the properties:
A DTD that asserts this property is the following:
If you have studied regular languages, regular expressions, and context-free grammars, then chances are that you wouldn't have any problem understanding what the previous DTD says. Loosely, each rule (i.e. V -> e, where V is a "label" in Σ and e is a regular expression over Σ) specifies that a V-labeled node in an unranked tree T has children with labels c1, ..., cn that can be generated by e. The Kleene star '*' stands for "zero or more". The question mark '?' abbreviates "zero or one". Commas ',' mean "followed by" in the sense of string concatenation. Finally, the symbol 'ε' is the empty string. Therefore, formally, a DTD over Σ is a pair (r,P) where r is the root symbol in Σ and P is a set of rules over Σ such that r does not appear in the "body" of any rules in P (i.e. on the right hand side).
Although DTD is a nice practical specification language for XML, it does not satisfy some nice properties of both practical and theoretical interests. For example, the sets of trees that can be recognized by DTDs are not closed under unions and complementations. [Recall that regular languages are closed under unions, intersection, and complementation (see here for more closure properties of regular languages).] Also, DTDs do not recognize "contexts" (e.g. how do you create a DTD that uses the tag "name" to mean two different things such as "name" of a "book", which should have no children, and "name" of a "person", which should have exactly two children labeled "First Name" and "Last Name"?). Nonetheless, this problem does not seem to bother programmers that much. This explains why DTD is still the most popular XML validation language. However, there are some XML validation languages that address the aforementioned problems. I believe the most popular such language is XSD (XML Schema Definition). We shall consider a formal model of XSD next. We shall later see that XSD has the full power of the yardstick logic for XML validation, which is monadic second-order logic.
Roughly speaking, the aim of validation is to ensure that an XML document "makes sense". More precisely, the problem is that, given an XML document (i.e. a labeled unranked tree T) and a statement f in some specification language L, we want to test whether T satisfies f. The most frequently used language L for validation of XML documents is DTD (Document Type Definition). Here, we use a formal model of DTDs that does not incorporate XML "data values", e.g., texts within XML tags (see my previous post). Let us start with an example. As always, we fix a finite alphabet Σ of discourse. Continuing with our example in the previous post, suppose we want to test whether an unranked tree T satisfies the properties:
- its root is labeled "books",
- every node labeled "books" may have zero or more children labeled "book", and
- every node labeled "book" must have four children labeled "title", "author", "year", and "publisher" (in this order), optionally followed by one child labeled "rank".
A DTD that asserts this property is the following:
books -> book*
book -> title, author, year, publisher, rank?
title -> ε
author -> ε
year -> ε
publisher -> ε
rank -> ε
If you have studied regular languages, regular expressions, and context-free grammars, then chances are that you wouldn't have any problem understanding what the previous DTD says. Loosely, each rule (i.e. V -> e, where V is a "label" in Σ and e is a regular expression over Σ) specifies that a V-labeled node in an unranked tree T has children with labels c1, ..., cn that can be generated by e. The Kleene star '*' stands for "zero or more". The question mark '?' abbreviates "zero or one". Commas ',' mean "followed by" in the sense of string concatenation. Finally, the symbol 'ε' is the empty string. Therefore, formally, a DTD over Σ is a pair (r,P) where r is the root symbol in Σ and P is a set of rules over Σ such that r does not appear in the "body" of any rules in P (i.e. on the right hand side).
Although DTD is a nice practical specification language for XML, it does not satisfy some nice properties of both practical and theoretical interests. For example, the sets of trees that can be recognized by DTDs are not closed under unions and complementations. [Recall that regular languages are closed under unions, intersection, and complementation (see here for more closure properties of regular languages).] Also, DTDs do not recognize "contexts" (e.g. how do you create a DTD that uses the tag "name" to mean two different things such as "name" of a "book", which should have no children, and "name" of a "person", which should have exactly two children labeled "First Name" and "Last Name"?). Nonetheless, this problem does not seem to bother programmers that much. This explains why DTD is still the most popular XML validation language. However, there are some XML validation languages that address the aforementioned problems. I believe the most popular such language is XSD (XML Schema Definition). We shall consider a formal model of XSD next. We shall later see that XSD has the full power of the yardstick logic for XML validation, which is monadic second-order logic.
Sunday, November 27, 2005
Australia qualified for the World Cup 2006 in Germany

After 30 years of bad luck, Australia has finally qualified for next year's World Cup in Germany after beating Uruguay in a dramatic penalty shoot-out at Sydney's Telstra Stadium, Australia.
Sunday, November 20, 2005
XML = Automata + Logic + Database
What do you get when you mix automata theory, mathematical logic, and database theory in a big bowl, and stir it vigorously? The answer is foundations of XML. In the past 7 - 8 years, the study of XML has generated a large number of elegant and unexpected connections between the three aforementioned areas. How so? Answer: we can view XML documents as labeled unranked trees, and we have numerous formalisms in (tree) automata theory and mathematical logic for querying and manipulating tree-like structures.
I presume you all know a little bit about HTML. XML is just like HTML but you have to define your own tags (e.g. <tag> ... </tag>). According to W3C XML tutorial, unlike HTML, whose primary goal is to display data focusing on how it looks, XML was designed to describe data and to focus on what data is. Well, then, what can you use XML for? Primarily, for information exchange on the web. In fact, one of the greatest promises of XML is to serve as the lingua franca in information exchange. Without further ado, let's look at an example of XML documents:
One can view this document as a labeled unranked tree:
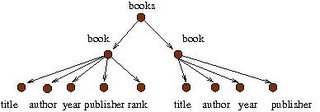
When we study foundations of XML, we care only about the structure of the tree. Consequently, we omitted the texts within the innermost tags. By definition, this tree is different from the tree that you get from exchanging the two children of "books". That is, a sibling ordering is assumed. Also, note that a node in an XML tree may have an arbitrarily large number of children. This is why the tree is said to be unranked.
We are interested in both procedural formalisms (i.e. automata) and logical formalisms (i.e. logical languages) for querying unranked trees. The intention is that we express the query in a logical language, which will then be converted to an automaton that one can run to compute the query against the XML document.
Of course, we should ask why we want to have query languages in the first place. Some answers are:
For validation, the yardstick logic is monadic second-order logic (MSO). This is because MSO is essentially equivalent to XSD (XML Schema Definition) which people use for validation in practice. For navigation, the yardstick logic is first-order logic (FO). This is because FO and its fragments is closely connected to XPath, a practical XML navigational language which people use.
What kind of procedural formalisms do we have for validation and navigation? For validation, we have what we call nondeterministic unranked tree automaton (NUTA). Its connection to MSO is very tight:
Theorem: A set of unranked trees (over a fixed finite set of labels) is recognizable by a NUTA iff it is definable in MSO.
What about navigation? This is still open.
Another research direction in foundations of XML concerns finding logics, which are equivalent to the yardstick logics, whose model-checking/query evaluation is polynomial in the size of the formula and tree. It is known that both MSO and FO have horrible complexity for model-checking over trees. Research in this direction often requires one to use some kinds of modal logics. For example, we know that CTL* (Computational Tree Logic*) with past operator, which researchers in model-checking community love, is equivalent to FO over unranked trees. There are also other research directions with a plethora of interesting open problems (such as streaming XML documents). If the reader is interested, I will further elaborate on foundations of XML.
I presume you all know a little bit about HTML. XML is just like HTML but you have to define your own tags (e.g. <tag> ... </tag>). According to W3C XML tutorial, unlike HTML, whose primary goal is to display data focusing on how it looks, XML was designed to describe data and to focus on what data is. Well, then, what can you use XML for? Primarily, for information exchange on the web. In fact, one of the greatest promises of XML is to serve as the lingua franca in information exchange. Without further ado, let's look at an example of XML documents:
<books>
<book>
<title>Elements of Finite Model Theory</title>
<author>Leonid Libkin</author>
<year>2004</year>
<publisher>Springer</publisher>
<rank>5/5</rank>
</book>
<book>
<title>Animal Farm</title>
<author>George Orwell</author>
<year>2003</year>
<publisher>Penguin Books</publisher>
</book>
</books>
One can view this document as a labeled unranked tree:

When we study foundations of XML, we care only about the structure of the tree. Consequently, we omitted the texts within the innermost tags. By definition, this tree is different from the tree that you get from exchanging the two children of "books". That is, a sibling ordering is assumed. Also, note that a node in an XML tree may have an arbitrarily large number of children. This is why the tree is said to be unranked.
We are interested in both procedural formalisms (i.e. automata) and logical formalisms (i.e. logical languages) for querying unranked trees. The intention is that we express the query in a logical language, which will then be converted to an automaton that one can run to compute the query against the XML document.
Of course, we should ask why we want to have query languages in the first place. Some answers are:
- Validation - we wish to distinguish XML documents that make sense and those that don't. A common example arises when two parties want to exchange some information using XML documents. They of course have to agree on the formatting of the documents that they accept. Elaborating on the example above, one may insist that "books" have zero or more children with tags "book", each of which must have four children with tags (in order) "title", "author", "year", and "publisher", and one optional child with tags "rank".
- Navigation. For example, one may want to ask for all nodes in the document that are tagged "book" and have a child tagged "rank".
For validation, the yardstick logic is monadic second-order logic (MSO). This is because MSO is essentially equivalent to XSD (XML Schema Definition) which people use for validation in practice. For navigation, the yardstick logic is first-order logic (FO). This is because FO and its fragments is closely connected to XPath, a practical XML navigational language which people use.
What kind of procedural formalisms do we have for validation and navigation? For validation, we have what we call nondeterministic unranked tree automaton (NUTA). Its connection to MSO is very tight:
Theorem: A set of unranked trees (over a fixed finite set of labels) is recognizable by a NUTA iff it is definable in MSO.
What about navigation? This is still open.
Another research direction in foundations of XML concerns finding logics, which are equivalent to the yardstick logics, whose model-checking/query evaluation is polynomial in the size of the formula and tree. It is known that both MSO and FO have horrible complexity for model-checking over trees. Research in this direction often requires one to use some kinds of modal logics. For example, we know that CTL* (Computational Tree Logic*) with past operator, which researchers in model-checking community love, is equivalent to FO over unranked trees. There are also other research directions with a plethora of interesting open problems (such as streaming XML documents). If the reader is interested, I will further elaborate on foundations of XML.
Saturday, November 12, 2005
Upcoming theory talk at UofT
For those of you in Toronto, you might want to stop by at UofT next Friday for a talk on P vs. NP. Here is the description:
Title: Can the P vs NP question be independent of the axioms of mathematical reasoning?
Speaker: Shai Ben-David, University of Waterloo
Venue: Galbraith Bld, Rm. 248
Time: 18 November, 11.10 AM
Abstract:
I'll discuss the possibility that the failure to resolve basic complexity theoretic statements stems from these statements being independent of the logical theories that underly our mathematical reasoning. In the first part of the talk, I shall briefly survey independence (from the axioms of set theory) of questions in various areas of mathematics. I shall then go on to discuss independence results that seem relevant to the P vs NP question. Finally, I shall outline some results of myself and Shai Halevi that imply that, as far as current proof techniques for such questions go, the task of proving that P vs NP is independent of Peano Arithmetic is as hard as proving very strong upper bounds on the (deterministic) complexity of the SAT problem.
Title: Can the P vs NP question be independent of the axioms of mathematical reasoning?
Speaker: Shai Ben-David, University of Waterloo
Venue: Galbraith Bld, Rm. 248
Time: 18 November, 11.10 AM
Abstract:
I'll discuss the possibility that the failure to resolve basic complexity theoretic statements stems from these statements being independent of the logical theories that underly our mathematical reasoning. In the first part of the talk, I shall briefly survey independence (from the axioms of set theory) of questions in various areas of mathematics. I shall then go on to discuss independence results that seem relevant to the P vs NP question. Finally, I shall outline some results of myself and Shai Halevi that imply that, as far as current proof techniques for such questions go, the task of proving that P vs NP is independent of Peano Arithmetic is as hard as proving very strong upper bounds on the (deterministic) complexity of the SAT problem.
Monday, November 07, 2005
Favorite Logic of November 2005: Second-Order Logic
Last month we talked about monadic second-order logic (MSO). We now shall proceed to a more expressive logic: second-order logic (SO) and some of its fragments, such as existential second-order logic (ESO) and universal second-order logic (ASO). In fact, some of the most tantalizing open questions in complexity theory can be reduced to questions about the expressive power of the afore-mentioned logics. More precisely, ESO equals NP, whereas ASO equals coNP. Hence, to separate P from NP, it is sufficient to prove that ASO and ESO have different expressive power. Since we have numerous tools for proving inexpressibility results in finite model theory, it is natural to ask whether it is possible to separate NP from coNP using finite model theory. This, as you would have expected, is still open. However, we have managed to prove a weaker version: that Monadic NP is different from Monadic coNP.
So, what exactly is SO? MSO permits quantifications over sets (i.e. unary relations). SO is just a generalization of this idea: you are allowed to quantify over k-ary relations. So, formulas in SO will look like
ψ := Q1X1...QmXm φ
where Q ∈ {∃,∀}, Xi is a ki-ary "second-order variable" to be interpreted as a ki-ary relation, and φ is just a first-order (FO) formula that talks about these second-order variables as well as some relations in the given vocabulary. An example of a sentence in this logic has been given in here, in which case all second-order variables are unary. Another example that uses non-unary relations is hamiltonianicity:
∃ L ∃ S ( (L is a strict linear ordering over the vertices) and (S is L's successor relation) and ∀ x ∀ y( S(x,y) -> E(x,y) ) )
A graph is hamiltonian iff there exists a path that visits every vertex in the graph. You can think of L as the transitive closure of the path P that witnesses the hamiltonianicity of the graph, and of S as the path P. [Example: a strict linear ordering on {1,2,3} is the binary relation ≤ = {(1,2),(1,3),(2,3)}, while its successor relation is the binary relation {(1,2),(2,3)}. Perhaps, it is more descriptive to say "immediate successor" than just "successor".] Notice that in these two examples we only used ∃ quantifiers for the second-order variables. We use ESO (read: existential second-order logic) to denote all formulas in SO of this kind, i.e., where all the Qi is ∃. We use ASO (read: universal second-order logic) to denote formulas in SO where Qi equals ∀.
Theorem (Fagin 1974): ESO captures NP. ASO captures coNP.
The notion of "capture" here has been defined in a previous post. The examples above give two concrete NP properties (hamiltonianicity, and 3-colorability) that you can express in ESO. How do you express non-hamiltonianicity in ASO? It's simple: just negate the formula above and use the fact that "not ∃ Xi ψ" is equivalent to "∃ Xi not &psi". This can easily be generalized to other coNP properties. Let's summarize the results.
Theorem: NP = coNP iff ESO = ASO iff 3-colorability is expressible in ASO.
What complexity class does SO correspond to?
Theorem (Stockmeyer 1977) SO captures PH.
Actually, Stockmeyer proved a much stronger result relating the kth level in the hierarchy to an SO fragment that contains formulas with k second-order quantifier alternation.
Of course, we have not been successful in proving that ESO != ASO. However, a weaker version has been proven in the literature.
Theorem (Fagin 1975) Monadic NP is different from Monadic coNP.
By monadic NP, we mean ESO formulas all of whose second-order variables are unary. The same goes for monadic coNP. So, monadic NP is just existential monadic second-order logic (EMSO), while monadic coNP is universal MSO (AMSO). The separation query given in Fagin's proof was "graph connectivity"; it is expressible in AMSO, but not in EMSO. A simplified version of this proof has been given in a paper by Ajtai, Fagin, and Stockmeyer (AFS) in 1995. [Correction: the paper is by Fagin, Stockmeyer, and Vardi (FSV) instead. Thanks to Ron Fagin for pointing this out.] In my opinion, this is also the most beatiful proof I have ever seen in finite model theory: simple, but extremely powerful. In a nutshell, this proof cleverly employs hanf-locality (which I have discussed here) which gives us a way of easily providing a winning strategy in "Ehrenfeucht-Fraisse games", which can be used to prove inexpressibility results. Is it possible to generalize the proof technique to ESO? Unfortunately no: Hanf-locality is not useful as soon as we permit binary second-order variables. On the other hand, we still have Ehrenfeucht-Fraisse games, which are in general hard to play. So, FSV proposed the following project: develop tools to easily establish a winning strategy in Ehrenfeucht-Fraisse games! Thus far, most tools of this kind uses some notions of locality, which is only useful for "sparse" structures. I hope that a more powerful tool can be discovered some time in the near future to prove a separation of ESO from ASO, although it seems that we are far from it.
The best way to learn AFS techniques for separating NP and coNP is to read Ron Fagin's
Easier ways to win logical games, DIMACS 1997
It is available from his website. A more complete reference is Leonid Libkin's excellent textbook titled Elements of Finite Model Theory (see chapter (3,4, and) 7).
So, what exactly is SO? MSO permits quantifications over sets (i.e. unary relations). SO is just a generalization of this idea: you are allowed to quantify over k-ary relations. So, formulas in SO will look like
ψ := Q1X1...QmXm φ
where Q ∈ {∃,∀}, Xi is a ki-ary "second-order variable" to be interpreted as a ki-ary relation, and φ is just a first-order (FO) formula that talks about these second-order variables as well as some relations in the given vocabulary. An example of a sentence in this logic has been given in here, in which case all second-order variables are unary. Another example that uses non-unary relations is hamiltonianicity:
∃ L ∃ S ( (L is a strict linear ordering over the vertices) and (S is L's successor relation) and ∀ x ∀ y( S(x,y) -> E(x,y) ) )
A graph is hamiltonian iff there exists a path that visits every vertex in the graph. You can think of L as the transitive closure of the path P that witnesses the hamiltonianicity of the graph, and of S as the path P. [Example: a strict linear ordering on {1,2,3} is the binary relation ≤ = {(1,2),(1,3),(2,3)}, while its successor relation is the binary relation {(1,2),(2,3)}. Perhaps, it is more descriptive to say "immediate successor" than just "successor".] Notice that in these two examples we only used ∃ quantifiers for the second-order variables. We use ESO (read: existential second-order logic) to denote all formulas in SO of this kind, i.e., where all the Qi is ∃. We use ASO (read: universal second-order logic) to denote formulas in SO where Qi equals ∀.
Theorem (Fagin 1974): ESO captures NP. ASO captures coNP.
The notion of "capture" here has been defined in a previous post. The examples above give two concrete NP properties (hamiltonianicity, and 3-colorability) that you can express in ESO. How do you express non-hamiltonianicity in ASO? It's simple: just negate the formula above and use the fact that "not ∃ Xi ψ" is equivalent to "∃ Xi not &psi". This can easily be generalized to other coNP properties. Let's summarize the results.
Theorem: NP = coNP iff ESO = ASO iff 3-colorability is expressible in ASO.
What complexity class does SO correspond to?
Theorem (Stockmeyer 1977) SO captures PH.
Actually, Stockmeyer proved a much stronger result relating the kth level in the hierarchy to an SO fragment that contains formulas with k second-order quantifier alternation.
Of course, we have not been successful in proving that ESO != ASO. However, a weaker version has been proven in the literature.
Theorem (Fagin 1975) Monadic NP is different from Monadic coNP.
By monadic NP, we mean ESO formulas all of whose second-order variables are unary. The same goes for monadic coNP. So, monadic NP is just existential monadic second-order logic (EMSO), while monadic coNP is universal MSO (AMSO). The separation query given in Fagin's proof was "graph connectivity"; it is expressible in AMSO, but not in EMSO. A simplified version of this proof has been given in a paper by Ajtai, Fagin, and Stockmeyer (AFS) in 1995. [Correction: the paper is by Fagin, Stockmeyer, and Vardi (FSV) instead. Thanks to Ron Fagin for pointing this out.] In my opinion, this is also the most beatiful proof I have ever seen in finite model theory: simple, but extremely powerful. In a nutshell, this proof cleverly employs hanf-locality (which I have discussed here) which gives us a way of easily providing a winning strategy in "Ehrenfeucht-Fraisse games", which can be used to prove inexpressibility results. Is it possible to generalize the proof technique to ESO? Unfortunately no: Hanf-locality is not useful as soon as we permit binary second-order variables. On the other hand, we still have Ehrenfeucht-Fraisse games, which are in general hard to play. So, FSV proposed the following project: develop tools to easily establish a winning strategy in Ehrenfeucht-Fraisse games! Thus far, most tools of this kind uses some notions of locality, which is only useful for "sparse" structures. I hope that a more powerful tool can be discovered some time in the near future to prove a separation of ESO from ASO, although it seems that we are far from it.
The best way to learn AFS techniques for separating NP and coNP is to read Ron Fagin's
Easier ways to win logical games, DIMACS 1997
It is available from his website. A more complete reference is Leonid Libkin's excellent textbook titled Elements of Finite Model Theory (see chapter (3,4, and) 7).
Lance Fortnow's ComplexityCast
Check out Lance Fortnow's ComplexityCast, in which he and Bill Gasarch engaged in an after-dinner talk about P vs. NP. I think it's really fun!
Friday, November 04, 2005
NL != P?
Howdy! It's been some time since I posted last. Being a graduate student, I don't think it is possible for me to post 3 - 4 times per week without sacrificing the quality of the posts. [Maybe, successful bloggers, like Professor Lance Fortnow, would care to tell me how they manage to cope well with both blogging and academic life.] However, my dear readers, rest assured! I do love posting here, and will try to post at least once a week.
Anyway, I just remembered that Stephen Cook told me some time ago that Michael Taitslin claimed to have a proof that NL is different from P, and at that time Steve was checking his proof. His paper can be found here. I am not quite sure of the progress. Incidentally, when I was in Los Alamos a couple of months back, a complexity theorist briefly looked at the paper and told me that it looks "fishy". Of course, in view of the many fallacious proofs that P != NP claimed by some novices (as discussed in here, people often tend to avoid reading "proofs" of this type of statements. Again, I am not sure of Taitslin's "proof". I read the first few pages, and all I can say is that he definitely uses some logic. One thing I can say though is that he has published some nice results in the areas of database theory and finite model theory in well-known journals and conference proceedings. This gives him some credentials, which perhaps will attract some of the readers to read his manuscript and find subtle bugs in his proof or verify the validity of his proof. In any case, if you decide to do so, please keep me informed :-)
Anyway, I just remembered that Stephen Cook told me some time ago that Michael Taitslin claimed to have a proof that NL is different from P, and at that time Steve was checking his proof. His paper can be found here. I am not quite sure of the progress. Incidentally, when I was in Los Alamos a couple of months back, a complexity theorist briefly looked at the paper and told me that it looks "fishy". Of course, in view of the many fallacious proofs that P != NP claimed by some novices (as discussed in here, people often tend to avoid reading "proofs" of this type of statements. Again, I am not sure of Taitslin's "proof". I read the first few pages, and all I can say is that he definitely uses some logic. One thing I can say though is that he has published some nice results in the areas of database theory and finite model theory in well-known journals and conference proceedings. This gives him some credentials, which perhaps will attract some of the readers to read his manuscript and find subtle bugs in his proof or verify the validity of his proof. In any case, if you decide to do so, please keep me informed :-)
Saturday, October 29, 2005
Favorite Logic of October 2005: Monadic Second-Order Logic
previous
We now move to a logic that is much more expressive than FO. In the previous "Favorite Logic" posts, I have talked about the gory details of FO. Now, rather than babble about the current logic under consideration, I shall just sample some results that are particularly interesting from my point of view. The readers that happen to be "inspired" by this post are welcome to send me an email for further results or references.
Monadic second-order logic (MSO) is a natural extension of first-order logic with quantifiers over sets of elements in the universe. More precisely, if σ is a vocabulary, MSO sentences ψ over σ are of the form
ψ := Q1X1...QmXm φ
where Qi ∈ {∃,∀}, Xi is a second-order variable, and φ is an FO sentence over σ ∪ {Xi: 1 ≤ i ≤ m}. So, that's the syntax. I will define the semantics by means of an example, the reader should be able to generalize easily.
Suppose σ = {E} is just a vocabulary with one binary relation symbol. We wish to express 2-colorability, i.e., the property
2COL = { G : G is a 2-colorable graph }
It can be proved that 2COL is inexpressible in FO. But, is it expressible in MSO? Positive.
∃ X ∃ Y( (X and Y partitions the vertex-set) and (any two adjacent vertices cannot both belong to X or Y) )
Suppose we are given a graph G = (V,E). Then, we can evaluate this formula as follows: this formula is true in G iff there exist unary relations (i.e. sets) X and Y over G (i.e. X, Y ⊆ V) such that the body of this formula evaluates to true in the structure (V,E,X,Y) (i.e. iff G is 2-colorable). In this case, we intend X and Y to correspond to the two color classes that partition the vertex-set.
The first conjunct above can be expressed by the FO sentence ∀x( X(x) <-> Y(x) ). As an exercise, the reader might enjoy coming up with an FO formula that expresses the second conjunct.
In fact, we can use the same trick to express k-colorability in MSO. Hence, we can immediately conclude that model-checking for MSO is NP-hard when only the models are part of the input (i.e. data-complexity is NP-hard). In fact, since MSO sentences are closed under negation, we also conclude that non-k-colorability is in MSO and therefore model-checking is coNP-hard as well.
Let's conclude this post with a beatiful result that connects MSO to formal language theory. The proof of the result can be found in Straubing's monograph
Finite Automata, Formal Logic, and Circuit Complexity
[Incidentally, David Molnar had a nice post that explores the connection between Straubing's result on "simulating monoids" and homomorphic cryptosystems. So, I thought it would be nice to mention a result from his book, although it was originally proven by Buchi in 1960s.] Roughly speaking, the result says:
A language (a set of strings) L is regular iff L is MSO-definable
What does it mean for a language to be MSO-definable? For notational convenience, let's restrict ourselves to the alphabet {0,1}. First, a binary string s = s0...sn-1 can be considered as a logical structure
S(s) := ({0,...,n-1}; <, U)
whose universe is {0,...,n-1} encoding the "positions" of the string, < is interpreted as the usual linear ordering over such universe, and U is a unary relation with the interpretation that i ∈ U iff si=1. So, if S(s) is a logical encoding of a string s and φ is a formula over the vocabulary {<,U}, the notion of 'S(s) |= φ' makes sense. The language defined by φ, then, is
{ s ∈ {0,1}* : S(s) |= φ }
Buchi's result says that MSO-definable languages are precisely regular languages. Doner, Thatcher, and Wright extended this result to trees:
A set of trees is regular iff it is definable in MSO.
These days, this result is widely employed in the area of "Foundations of XML", which have put automata, logic, and complexity theory under the same roof, which is no short of wondrous. If this interests you, take a loot at some surveys in here.
We now move to a logic that is much more expressive than FO. In the previous "Favorite Logic" posts, I have talked about the gory details of FO. Now, rather than babble about the current logic under consideration, I shall just sample some results that are particularly interesting from my point of view. The readers that happen to be "inspired" by this post are welcome to send me an email for further results or references.
Monadic second-order logic (MSO) is a natural extension of first-order logic with quantifiers over sets of elements in the universe. More precisely, if σ is a vocabulary, MSO sentences ψ over σ are of the form
ψ := Q1X1...QmXm φ
where Qi ∈ {∃,∀}, Xi is a second-order variable, and φ is an FO sentence over σ ∪ {Xi: 1 ≤ i ≤ m}. So, that's the syntax. I will define the semantics by means of an example, the reader should be able to generalize easily.
Suppose σ = {E} is just a vocabulary with one binary relation symbol. We wish to express 2-colorability, i.e., the property
2COL = { G : G is a 2-colorable graph }
It can be proved that 2COL is inexpressible in FO. But, is it expressible in MSO? Positive.
∃ X ∃ Y( (X and Y partitions the vertex-set) and (any two adjacent vertices cannot both belong to X or Y) )
Suppose we are given a graph G = (V,E). Then, we can evaluate this formula as follows: this formula is true in G iff there exist unary relations (i.e. sets) X and Y over G (i.e. X, Y ⊆ V) such that the body of this formula evaluates to true in the structure (V,E,X,Y) (i.e. iff G is 2-colorable). In this case, we intend X and Y to correspond to the two color classes that partition the vertex-set.
The first conjunct above can be expressed by the FO sentence ∀x( X(x) <-> Y(x) ). As an exercise, the reader might enjoy coming up with an FO formula that expresses the second conjunct.
In fact, we can use the same trick to express k-colorability in MSO. Hence, we can immediately conclude that model-checking for MSO is NP-hard when only the models are part of the input (i.e. data-complexity is NP-hard). In fact, since MSO sentences are closed under negation, we also conclude that non-k-colorability is in MSO and therefore model-checking is coNP-hard as well.
Let's conclude this post with a beatiful result that connects MSO to formal language theory. The proof of the result can be found in Straubing's monograph
Finite Automata, Formal Logic, and Circuit Complexity
[Incidentally, David Molnar had a nice post that explores the connection between Straubing's result on "simulating monoids" and homomorphic cryptosystems. So, I thought it would be nice to mention a result from his book, although it was originally proven by Buchi in 1960s.] Roughly speaking, the result says:
A language (a set of strings) L is regular iff L is MSO-definable
What does it mean for a language to be MSO-definable? For notational convenience, let's restrict ourselves to the alphabet {0,1}. First, a binary string s = s0...sn-1 can be considered as a logical structure
S(s) := ({0,...,n-1}; <, U)
whose universe is {0,...,n-1} encoding the "positions" of the string, < is interpreted as the usual linear ordering over such universe, and U is a unary relation with the interpretation that i ∈ U iff si=1. So, if S(s) is a logical encoding of a string s and φ is a formula over the vocabulary {<,U}, the notion of 'S(s) |= φ' makes sense. The language defined by φ, then, is
{ s ∈ {0,1}* : S(s) |= φ }
Buchi's result says that MSO-definable languages are precisely regular languages. Doner, Thatcher, and Wright extended this result to trees:
A set of trees is regular iff it is definable in MSO.
These days, this result is widely employed in the area of "Foundations of XML", which have put automata, logic, and complexity theory under the same roof, which is no short of wondrous. If this interests you, take a loot at some surveys in here.
Monday, October 24, 2005
Let's play games
About a month ago I saved a draft on the complexity of games in finite model theory. Suddenly, this morning David Eppstein left a comment on my previous post, which reminded me about this draft. Incidentally, I have been a fan of his recreational math pages, especially the combinatorial game theory page, since two years ago, after taking a course on the theory of computation. Anyway, let's play some games now! The games that we will play are not something I invent myself ;-). They are actually pervasive in finite model theory.
Here is the description. Two graphs G and G', and a natural number k are given. There are two players in this game, Spoiler and Duplicator. They will play for k rounds. In the i'th round (1 ≤ i ≤ k), Spoiler starts by picking a vertex in one of the graphs. Then, Duplicator will have to respond by picking a vertex in the other graph. After k rounds have been played, we obtain the vertices a0, ..., ak of G, and the vertices b0, ..., bk of G'. Duplicator is declared to be the winner if the subgraphs of G and G' that are induced by ai's and bj's are isomorphic. Otherwise, Spoiler wins. By the way, why are the players called Spoiler and Duplicator? If you think about this, Spoiler's goal is to show that the two graphs are not isomorphic (i.e. to spoil), while Duplicator's goal is to show that the two graphs are isomorphic by matching (or "duplicating") each of Spoiler's moves in such a way no difference in the two graphs are revealed. So, Duplicator is the "good" guy, while Spoiler is the "bad" guy. Duplicator has a winning strategy on this game if no matter how Spoiler moves in the i'th round, Duplicator can always find a move that will guarantee a "win" for Duplicator.
The problem is, given G, G', and k, decide whether Duplicator has a winning strategy. Determine its complexity! I will post the solution and some open problems later.
But, let me give you a simple example. Suppose G = Kk and G' = Kk+1. Then, it is easy to see that Duplicator has a winning strategy for the i-round game, where 0 ≤ i ≤ k (why?). However, a moment's thought will reveal that, for any i-round game on G and G' where i > k, Spoiler has a winning strategy. Where G and G' are more complicated structures, it becomes harder to decide whether Duplicator has a winning strategy.
Here is the description. Two graphs G and G', and a natural number k are given. There are two players in this game, Spoiler and Duplicator. They will play for k rounds. In the i'th round (1 ≤ i ≤ k), Spoiler starts by picking a vertex in one of the graphs. Then, Duplicator will have to respond by picking a vertex in the other graph. After k rounds have been played, we obtain the vertices a0, ..., ak of G, and the vertices b0, ..., bk of G'. Duplicator is declared to be the winner if the subgraphs of G and G' that are induced by ai's and bj's are isomorphic. Otherwise, Spoiler wins. By the way, why are the players called Spoiler and Duplicator? If you think about this, Spoiler's goal is to show that the two graphs are not isomorphic (i.e. to spoil), while Duplicator's goal is to show that the two graphs are isomorphic by matching (or "duplicating") each of Spoiler's moves in such a way no difference in the two graphs are revealed. So, Duplicator is the "good" guy, while Spoiler is the "bad" guy. Duplicator has a winning strategy on this game if no matter how Spoiler moves in the i'th round, Duplicator can always find a move that will guarantee a "win" for Duplicator.
The problem is, given G, G', and k, decide whether Duplicator has a winning strategy. Determine its complexity! I will post the solution and some open problems later.
But, let me give you a simple example. Suppose G = Kk and G' = Kk+1. Then, it is easy to see that Duplicator has a winning strategy for the i-round game, where 0 ≤ i ≤ k (why?). However, a moment's thought will reveal that, for any i-round game on G and G' where i > k, Spoiler has a winning strategy. Where G and G' are more complicated structures, it becomes harder to decide whether Duplicator has a winning strategy.
Sunday, October 23, 2005
Some links of interests
I have just added some new links to several interesting blogs to my blogroll: David Molnar's blog, Kurt Van Etten's, and Scott Aaronson's (the complexity zoo keeper). It's great to see that the blogging community grows very well. This comes at one price however: there is just no time to visit regularly every single interesting blog there is. There are just too many good ones these days!
Also, I have recently discovered a nice-looking online textbook on 'universal algebra'. I haven't read it yet, though. But, it has some nice applications to computer science (automata theory, rewriting systems, etc.) and model theory. If you are a complexity theorist, a motivation to look at this book may be Straubing's monograph
Finite Automata, Formal Logic, and Circuit Complexity (Progress in Theoretical Computer Science), Springer, 1994.
In this monograph, Straubing demonstrates the possibility of attacking tantalizing open problems in circuit complexity using automata theory, semigroup theory, and finite model theory. In fact, I have heard a rumour that Straubing very recently proved a separation result in complexity theory using this technique ...
Also, I have recently discovered a nice-looking online textbook on 'universal algebra'. I haven't read it yet, though. But, it has some nice applications to computer science (automata theory, rewriting systems, etc.) and model theory. If you are a complexity theorist, a motivation to look at this book may be Straubing's monograph
Finite Automata, Formal Logic, and Circuit Complexity (Progress in Theoretical Computer Science), Springer, 1994.
In this monograph, Straubing demonstrates the possibility of attacking tantalizing open problems in circuit complexity using automata theory, semigroup theory, and finite model theory. In fact, I have heard a rumour that Straubing very recently proved a separation result in complexity theory using this technique ...
Saturday, October 22, 2005
Strange things happen
Around this time last year I was busy preparing my applications to PhD programs in the U.K. and North America. In particular, University of Cambridge, which happened to be one of those universities I was interested in , requires each applicant to write a short research proposal. [As you of course know, I chose University of Toronto, which was my first preference all along.] So, I had a discussion with Anuj Dawar, who was the finite model theorist at Cambridge I wished to work with, on what sort of research directions to pursue for PhD studies. He gave me two research problems:
Don't worry if you don't know what they mean. The important thing to know is that both of these problems are long-standing open problems in the area. Both of these problems looked formidable to me then (and they still do now), and so I didn't bother thinking about them. Anyway, to my surprise, both of these problems have been resolved this year in quick succession. The first problem was solved positively by Benjamin Rossman, who this year just started his graduate school. His paper titled
Existential Positive Types and Preservation Under Homomorphisms
was recently published in this year's LICS proceeding and awarded Kleene's award for the best student paper. [Congratulation Ben!] You can find his paper on his web site. The second problem was very recently solved by Leonid Libkin, my supervisor. You have to wait if you want to get the paper.
I wish I had collaborated with these guys on these problems. D'oh!
- Homomorphism preservation theorem in the finite.
- Do order-invariant FO properties have the zero-one law?
Don't worry if you don't know what they mean. The important thing to know is that both of these problems are long-standing open problems in the area. Both of these problems looked formidable to me then (and they still do now), and so I didn't bother thinking about them. Anyway, to my surprise, both of these problems have been resolved this year in quick succession. The first problem was solved positively by Benjamin Rossman, who this year just started his graduate school. His paper titled
Existential Positive Types and Preservation Under Homomorphisms
was recently published in this year's LICS proceeding and awarded Kleene's award for the best student paper. [Congratulation Ben!] You can find his paper on his web site. The second problem was very recently solved by Leonid Libkin, my supervisor. You have to wait if you want to get the paper.
I wish I had collaborated with these guys on these problems. D'oh!
Thursday, October 20, 2005
Special Programmes on Logic and Algorithms in Cambridge
During the first half of next year, there will be a series of workshops on Logic and Algorithms (broadly construed) at Isaac Newton Institute for Mathematical Sciences (Cambridge). Looking at their workshop titles is enough to convince ourselves that there is something for everyone:
There will be quite a number of invited speakers from University of Toronto. They include Stephen Cook, Leonid Libkin, and Toniann Pitassi.
- Finite and Algorithmic Model Theory (9-13 January).
- Logic and Databases (27 February - 3 March).
- Mathematics of Constraint Satisfaction: Algebra, Logic, and Graph Theory (20-24 March).
- New Directions in Proof Complexity (10-13 April).
- Constraints and Verification (8-12 May).
- Games and Verification (3-7 July).
There will be quite a number of invited speakers from University of Toronto. They include Stephen Cook, Leonid Libkin, and Toniann Pitassi.
Monday, October 17, 2005
Logics capturing complexity classes
David Molnar asked a good question: (in my words) what does it mean to have a logic for a complexity class over ordered structures and over all (i.e. both ordered and unordered) structures? To answer this question, I will have to define what it means for a logic to capture a complexity class. As always, I assume that you have read preliminaries 1 and 2, which can be accessed from the sidebar. [Please let me know if your browser has any problem displaying the symbols.]
We will first recall the definition of "expressibility" of a property in a logic. Suppose we are given a σ-property (or boolean query) Q over a class C of σ-structures, i.e., Q is just a subset of C. Then, Q is said to be expressible in a logic L over C if there exists an L-sentence f such that, for any A ∈ C, A ∈ Q iff A |= f. When C is not mentioned, C is assumed to be the class of all finite σ-structures.
Observe that one can think of boolean queries as an analogue of the notion of languages, in the sense of formal language theory, or, more loosely, "computational problems". For example, consider the problem of testing hamiltonianicity of a graph. We can think of this problem as a boolean query H over the graph vocabulary such that a (finite) graph is in H iff it is hamiltonian. As a matter of fact, it is possible to encode any σ-structure as a (binary) string, and a string as a τ-structure for some vocabulary τ. Therefore, we can view any σ-boolean query as a language, and vice versa. So, we may redefine any complexity class K to be the set of all σ-properties that are computable in K, where σ ranges over all relational vocabularies. Hence, PTIME is the set of boolean queries that are computable in polynomial-time. For convenience, given a class C of structures, we also define KC to be the set of properties Q that are computable in K, when we restrict the input to Q to be all structures in C that have the same vocabulary as Q. When C is not mentioned, we assume C to be the set of all finite structures.
We are now ready to define the most important definition in descriptive complexity. A logic L is said to capture a complexity class K over a class C of finite structures if for any Q ∈ C: Q ∈ KC iff Q is expressible in L over C. Again, when C is not mentioned, it is assumed to be the set of all finite structures.
We know that existential second-order logic (ESO) captures NP. This is Fagin's result, which was discussed in Lance's blog recently. On the other hand, it is open whether there exists a logic that captures PTIME. We know, however, that there exists a logic (FO+LFP: first-order logic + least fixed point operator) that captures PTIME over all ordered structures. [Ordered structures mean that, we assume a binary relation in the structure to be interpreted as a total linear ordering on the universe.] This result was proven independently by Neil Immerman and Moshe Vardi in the 80's. You might be wondering whether FO+LFP captures PTIME. The answer is no: even testing whether a graph has an even number of elements cannot be done in FO+LFP without the help of an "external" linear order. The question whether there exists a logic for PTIME was first raised by Chandra and Harel in the 70's. Also, as I mentioned in a previous post, Yuri Gurevich conjectured that there is no logic for P (and this will imply that P ≠ NP). On a related note, it is also open whether there is a logic for any important complexity class below NP such as PTIME, L, NL, etc.
A relevant question is the following: why do we want to have a logic that capture complexity classes over all finite structures (not just over ordered structures)? The answer is technical: linear orderings make an inexpressibility proof more complicated by an order of magnitude!
We will first recall the definition of "expressibility" of a property in a logic. Suppose we are given a σ-property (or boolean query) Q over a class C of σ-structures, i.e., Q is just a subset of C. Then, Q is said to be expressible in a logic L over C if there exists an L-sentence f such that, for any A ∈ C, A ∈ Q iff A |= f. When C is not mentioned, C is assumed to be the class of all finite σ-structures.
Observe that one can think of boolean queries as an analogue of the notion of languages, in the sense of formal language theory, or, more loosely, "computational problems". For example, consider the problem of testing hamiltonianicity of a graph. We can think of this problem as a boolean query H over the graph vocabulary such that a (finite) graph is in H iff it is hamiltonian. As a matter of fact, it is possible to encode any σ-structure as a (binary) string, and a string as a τ-structure for some vocabulary τ. Therefore, we can view any σ-boolean query as a language, and vice versa. So, we may redefine any complexity class K to be the set of all σ-properties that are computable in K, where σ ranges over all relational vocabularies. Hence, PTIME is the set of boolean queries that are computable in polynomial-time. For convenience, given a class C of structures, we also define KC to be the set of properties Q that are computable in K, when we restrict the input to Q to be all structures in C that have the same vocabulary as Q. When C is not mentioned, we assume C to be the set of all finite structures.
We are now ready to define the most important definition in descriptive complexity. A logic L is said to capture a complexity class K over a class C of finite structures if for any Q ∈ C: Q ∈ KC iff Q is expressible in L over C. Again, when C is not mentioned, it is assumed to be the set of all finite structures.
We know that existential second-order logic (ESO) captures NP. This is Fagin's result, which was discussed in Lance's blog recently. On the other hand, it is open whether there exists a logic that captures PTIME. We know, however, that there exists a logic (FO+LFP: first-order logic + least fixed point operator) that captures PTIME over all ordered structures. [Ordered structures mean that, we assume a binary relation in the structure to be interpreted as a total linear ordering on the universe.] This result was proven independently by Neil Immerman and Moshe Vardi in the 80's. You might be wondering whether FO+LFP captures PTIME. The answer is no: even testing whether a graph has an even number of elements cannot be done in FO+LFP without the help of an "external" linear order. The question whether there exists a logic for PTIME was first raised by Chandra and Harel in the 70's. Also, as I mentioned in a previous post, Yuri Gurevich conjectured that there is no logic for P (and this will imply that P ≠ NP). On a related note, it is also open whether there is a logic for any important complexity class below NP such as PTIME, L, NL, etc.
A relevant question is the following: why do we want to have a logic that capture complexity classes over all finite structures (not just over ordered structures)? The answer is technical: linear orderings make an inexpressibility proof more complicated by an order of magnitude!
Saturday, October 15, 2005
Fun Proof Techniques
About three years ago, I took a course on the theory of computation. I remember that during the second lecture, our instructor introduced us to the mathematical background, and in particular proof techniques. He started saying "in mathematics, we have proof by induction, proof by construction, and proof by contradiction ...". Before he finished the lecture, he presented to us a list of fun proof techniques which work in practice, some of which are listed here. My favorite ones are:
What are your favorite proof techniques?
- Proof by blatant assertion: this is marked by expressions like "obviously", "trivially", "any moron can see that".
- Proof by example: you sketch a proof that the theorem is true for n = 4, and claim that this proof generalizes to all n.
- Proof by picture: picture + handwaving makes a pretty compelling argument in a classroom.
- Proof by omission: we state the theorem and the proof is left as an exercise for the reader.
- Proof by accumulated evidence: for three decades we have worked very hard to produce an efficient algorithm for NP-complete problems without results; therefore P != NP.
- Proof by reference to famous people: I saw Karp on the elevator, and he thought that our problem is NP-complete!
- Proof by confusion: P = NP <=> P - NP = 0 <=> P(1-N) = 0 <=> P = 0 or N = 1; but the last expression is false and therefore P != NP.
What are your favorite proof techniques?
An approach to prove P != NP
Let K be a complexity class. We wish to recursively enumerate exactly those "graph languages" that can be decided in K. By graph languages, we mean languages whose inputs are graphs (say in adjacency matrix format) such that two isomorphic graphs are either both in the language or both not in the language. So, graph languages are "closed under isomorphisms". If this can be done for K, we say that the set of K graph properties is recursively indexable.
The set of NP graph properties is known to be recursively indexable. This is due to the fact that we have a logic for NP (i.e. existential second-order logic). On the other hand, it is a long-standing open problem whether P graph properties are recursively indexable. [No, you can't use the usual enumeration for clocked poly-time Turing machines as they contain "bad" graph languages.] Of course, the existence of a logic for P, which is another big open problem in finite model theory, will imply that P graph properties are recursively indexable. [(LFP+<)inv captures PTIME properties over ordered structures only.] Yuri Gurevich conjectured that P graph properties are not recursively indexable, and therefore, there is no logic for P. See his paper. In particular, if the conjecture is true, then P is different from NP as NP graph properties are recursively indexable! So, try to prove that P graph properties are not recursively indexable!
The set of NP graph properties is known to be recursively indexable. This is due to the fact that we have a logic for NP (i.e. existential second-order logic). On the other hand, it is a long-standing open problem whether P graph properties are recursively indexable. [No, you can't use the usual enumeration for clocked poly-time Turing machines as they contain "bad" graph languages.] Of course, the existence of a logic for P, which is another big open problem in finite model theory, will imply that P graph properties are recursively indexable. [(LFP+<)inv captures PTIME properties over ordered structures only.] Yuri Gurevich conjectured that P graph properties are not recursively indexable, and therefore, there is no logic for P. See his paper. In particular, if the conjecture is true, then P is different from NP as NP graph properties are recursively indexable! So, try to prove that P graph properties are not recursively indexable!
Thursday, October 13, 2005
Favorite Logic of September 2005: First-order Logic (3)
previous|
next
We are somewhat behind our schedule. So, let's close it out now. This post concludes our series of posts on first-order logic as the favorite logic of last month (oops!). I will give a glimpse of the expressiveness of first-order logic, and tools for showing inexpressibility results. The literature on this topic is so vast that it is impossible to cover all possible results and tools; so, I will mention only a selection of results and tools, and give examples on how to apply the tools mentioned. Also, see the preliminaries before reading this post.
Let's get right down to business. Our main problem can be described as follows: suppose Q is a σ-property (i.e. boolean query), and we want to know whether there exists a first-order sentence that defines Q. If there is one, then it suffices to come up with a sentence f that defines Q. If not, what shall we do?
Well ... in model theory, we have a plethora of tools in our toolbox:
Let's try compactness on an example. Suppose we want to show that the property GC testing graph connectivity is not first-order definable. Suppose to the contrary that f defines GC. Then, consider the theory T = {f} ∪ { πn : n is positive nat. number } where πn is the first-order sentence
∃x∃y( there is no path of length n from x to y )
Clearly, this sentence is first-order. By compactness, it is easy to show that T is consistent (just take the biggest n for which πn appears in this finite subset of T and "elongate" the path from x to y by increasing the number of elements in the universe). So, we have a model M for T. But in M, x and y are not connected by a (finite) path, contradicting f. Therefore, f cannot be a first-order sentence.
That's short and simple! The problem, however, is that this doesn't prove that FO cannot express GC in the finite (i.e. the ground set of GC is restricted to all finite graphs only), as compactness theorem fails in the finite. So, how do we prove that GC cannot be expressed in the finite? It is a sad fact that most of the tools from model theory fails in the finite. Some of the few that survive include Ehrenfeucht-Fraisse game theorem, Gaifmann-locality, and Hanf-locality. Here we shall use the notion of Hanf-locality to prove that GC is not FO definable.
Let me try to intuitively illustrate the notion of Hanf-locality for graphs. A graph property P (over all finite structures) is said to be hanf-local if there exists a number d such that for every two finite graphs A and B:
that A and B d-locally look the same implies that A and B agree on P.
The smallest such number d is called hanf-locality rank of P. What do we mean by "d-locally look the same"? A and B d-locally look the same if there exists a bijection g from V(A) to V(B), the vertices of A and B, such that for every c in V(A) there exists an isomorphism from the d-neighborhood of A around c to the d-neighborhood of B around g(c) which maps c to g(c). That is, if you have only limited local vision (say up to d distance) and if you pick a spot c in the graph A, I can always give you another spot in the graph B (via the bijection) such that you cannot see the difference between your surroundings on these two different spots.
Now, our strategy for proving that GC is not first-order expressible is:
We won't prove item 1. We will however sketch how to prove item 2. Suppose GC is hanf-local with rank d. Then, define two graphs G and G' as follows. Take a number p >> d. G is a cycle with 2p nodes, and G' is a disjoint union of cycles each with p nodes. You can easily check that there is only one type of d-neighborhood (up to isomorphism) around any vertex c in G and G', i.e., the 2d+1-path with c right in the middle. So, just take any arbitrary bijection between G and G' to show that they d-locally look the same. However, G is connected but G' is not, contradicting the assumption that GC is hanf-local!
I would love to talk about Ehrenfeucht-Fraisse games and Gaifmann locality, which are equally important tools in finite model theory for proving FO inexpressibility. Sadly, this will only make this post longer than it already is. So, I will refer you to Leonid Libkin's Elements of Finite Model Theory for more on this (and also for the proper acknowledgement of these results!).
next
We are somewhat behind our schedule. So, let's close it out now. This post concludes our series of posts on first-order logic as the favorite logic of last month (oops!). I will give a glimpse of the expressiveness of first-order logic, and tools for showing inexpressibility results. The literature on this topic is so vast that it is impossible to cover all possible results and tools; so, I will mention only a selection of results and tools, and give examples on how to apply the tools mentioned. Also, see the preliminaries before reading this post.
Let's get right down to business. Our main problem can be described as follows: suppose Q is a σ-property (i.e. boolean query), and we want to know whether there exists a first-order sentence that defines Q. If there is one, then it suffices to come up with a sentence f that defines Q. If not, what shall we do?
Well ... in model theory, we have a plethora of tools in our toolbox:
- Compactness: a theory T is consistent iff every finite subset of T is consistent.
- (Restricted form of) Lowenheim-Skolem: If a theory has an infinite model, then it has a countable model.
Let's try compactness on an example. Suppose we want to show that the property GC testing graph connectivity is not first-order definable. Suppose to the contrary that f defines GC. Then, consider the theory T = {f} ∪ { πn : n is positive nat. number } where πn is the first-order sentence
∃x∃y( there is no path of length n from x to y )
Clearly, this sentence is first-order. By compactness, it is easy to show that T is consistent (just take the biggest n for which πn appears in this finite subset of T and "elongate" the path from x to y by increasing the number of elements in the universe). So, we have a model M for T. But in M, x and y are not connected by a (finite) path, contradicting f. Therefore, f cannot be a first-order sentence.
That's short and simple! The problem, however, is that this doesn't prove that FO cannot express GC in the finite (i.e. the ground set of GC is restricted to all finite graphs only), as compactness theorem fails in the finite. So, how do we prove that GC cannot be expressed in the finite? It is a sad fact that most of the tools from model theory fails in the finite. Some of the few that survive include Ehrenfeucht-Fraisse game theorem, Gaifmann-locality, and Hanf-locality. Here we shall use the notion of Hanf-locality to prove that GC is not FO definable.
Let me try to intuitively illustrate the notion of Hanf-locality for graphs. A graph property P (over all finite structures) is said to be hanf-local if there exists a number d such that for every two finite graphs A and B:
that A and B d-locally look the same implies that A and B agree on P.
The smallest such number d is called hanf-locality rank of P. What do we mean by "d-locally look the same"? A and B d-locally look the same if there exists a bijection g from V(A) to V(B), the vertices of A and B, such that for every c in V(A) there exists an isomorphism from the d-neighborhood of A around c to the d-neighborhood of B around g(c) which maps c to g(c). That is, if you have only limited local vision (say up to d distance) and if you pick a spot c in the graph A, I can always give you another spot in the graph B (via the bijection) such that you cannot see the difference between your surroundings on these two different spots.
Now, our strategy for proving that GC is not first-order expressible is:
- Show that every first-order definable query is hanf-local.
- Show that GC is not hanf-local.
We won't prove item 1. We will however sketch how to prove item 2. Suppose GC is hanf-local with rank d. Then, define two graphs G and G' as follows. Take a number p >> d. G is a cycle with 2p nodes, and G' is a disjoint union of cycles each with p nodes. You can easily check that there is only one type of d-neighborhood (up to isomorphism) around any vertex c in G and G', i.e., the 2d+1-path with c right in the middle. So, just take any arbitrary bijection between G and G' to show that they d-locally look the same. However, G is connected but G' is not, contradicting the assumption that GC is hanf-local!
I would love to talk about Ehrenfeucht-Fraisse games and Gaifmann locality, which are equally important tools in finite model theory for proving FO inexpressibility. Sadly, this will only make this post longer than it already is. So, I will refer you to Leonid Libkin's Elements of Finite Model Theory for more on this (and also for the proper acknowledgement of these results!).
Tuesday, October 11, 2005
Happy Thanksgiving!
Most of you in the U.S. might probably be bewildered by what I'm saying. However, yesterday was a thanksgiving day in Canada. This was my first encounter of any kind of "thanksgiving day" in my entire life as I am from Australia.
Anyway, I guess I will have to get used to this custom as I will be here for another 5 years. So, happy thanksgiving! Thanks to all of you who have left useful comments on my blog. I do learn a lot from all these comments.
Anyway, I guess I will have to get used to this custom as I will be here for another 5 years. So, happy thanksgiving! Thanks to all of you who have left useful comments on my blog. I do learn a lot from all these comments.
Lance's Recent Post on Fagin's Theorem
Lance Fortnow posted his favorite theorem of this month on his blog: it's Fagin's theorem, one of the most important results (and the first of its kind) in descriptive complexity theory. Nice!
Monday, October 10, 2005
Favorite Logic of September 2005: First-order Logic (2)
(previous|next)
Howdy! Today we will resume on our discussion of first-order logic. In particular, we will talk about model-checking.
Diving right in ... the problem is as follows: given a finite structure M and an FO formula f, we want to test whether M |= f, i.e., f is true in M. Immediately, I hear you say that this problem is trivially decidable as we can use the inductive definition of M |= f to do the testing. Well ... it is decidable, but we want to know its complexity. We won't talk about how to represent M, although it matters in this case, as we will only mention results. You can represent f in any way you like, e.g., the parse tree for f.
There are three common measures for the complexity of this problem:
Data complexity measure is commonly used in the field of databases, where usually M is very big and the query f is small. Combined complexity and expression complexity measure is commonly used in the area of verification (commonly called model-checking), where f can be very large and complex. If the reader is curious about any of these areas, I will gladly recommend "Foundations of Databases" by Abiteboul et al. and "Logic in Computer Science" by Huth et al.
It is not hard to analyze the running time of the algorithm for testing M |= f induced by the usual inductive definition of |=. You will get O(|f| x |M|^k) where k is the width of f, i.e., the maximum number of free variables in every subformula of f. So, k does depend on f. That is, the algorithm runs polynomial in |M| but exponential in |f|. In fact, one can show that the data complexity of this problem with respect to FO is AC^0, where as the expression and combined complexity is PSPACE-complete. As an exercise, the reader might want to try to prove the latter as it is quite simple (hint: reduce the problem QBF).
Papadimitriou and Yannakakis have an interesting paper that refines these complexity measures using the theory of parameterized complexity. The motivation of this paper is the following: although |f| << |M|, the fact that |f| is an exponent of |M| is no good because even for "small" |f|, say |f| = 20, an algorithm that runs in O(n^20) cannot be considered tractable (especially when n is really big, like in database applications). So, the question then is whether it is possible to have an algorithm for testing M |= f that runs in g(|f|)|M|^c where g is a function from natural numbers to natural numbers, and c is a constant independent of both |M| and |f|. The result of this paper essentially stipulates that any algorithm for evaluating M |= f must have |f| as an exponent of |M|, unless the W hierarchy collapses. See the following reference if interested:
On Complexity of Database Queries, Papadimitriou and Yannakakis, JCSS, Vol 58, 1999.
We will next talk about the expressive power of FO.
Howdy! Today we will resume on our discussion of first-order logic. In particular, we will talk about model-checking.
Diving right in ... the problem is as follows: given a finite structure M and an FO formula f, we want to test whether M |= f, i.e., f is true in M. Immediately, I hear you say that this problem is trivially decidable as we can use the inductive definition of M |= f to do the testing. Well ... it is decidable, but we want to know its complexity. We won't talk about how to represent M, although it matters in this case, as we will only mention results. You can represent f in any way you like, e.g., the parse tree for f.
There are three common measures for the complexity of this problem:
- Data Complexity: the input is M (i.e. f is fixed). So, we measure the performance of any algorithm for the problem in terms of |M| only.
- Expression complexity: the input is f (i.e. M is fixed).
- Combined complexity: the input is (M,f).
Data complexity measure is commonly used in the field of databases, where usually M is very big and the query f is small. Combined complexity and expression complexity measure is commonly used in the area of verification (commonly called model-checking), where f can be very large and complex. If the reader is curious about any of these areas, I will gladly recommend "Foundations of Databases" by Abiteboul et al. and "Logic in Computer Science" by Huth et al.
It is not hard to analyze the running time of the algorithm for testing M |= f induced by the usual inductive definition of |=. You will get O(|f| x |M|^k) where k is the width of f, i.e., the maximum number of free variables in every subformula of f. So, k does depend on f. That is, the algorithm runs polynomial in |M| but exponential in |f|. In fact, one can show that the data complexity of this problem with respect to FO is AC^0, where as the expression and combined complexity is PSPACE-complete. As an exercise, the reader might want to try to prove the latter as it is quite simple (hint: reduce the problem QBF).
Papadimitriou and Yannakakis have an interesting paper that refines these complexity measures using the theory of parameterized complexity. The motivation of this paper is the following: although |f| << |M|, the fact that |f| is an exponent of |M| is no good because even for "small" |f|, say |f| = 20, an algorithm that runs in O(n^20) cannot be considered tractable (especially when n is really big, like in database applications). So, the question then is whether it is possible to have an algorithm for testing M |= f that runs in g(|f|)|M|^c where g is a function from natural numbers to natural numbers, and c is a constant independent of both |M| and |f|. The result of this paper essentially stipulates that any algorithm for evaluating M |= f must have |f| as an exponent of |M|, unless the W hierarchy collapses. See the following reference if interested:
On Complexity of Database Queries, Papadimitriou and Yannakakis, JCSS, Vol 58, 1999.
We will next talk about the expressive power of FO.
Saturday, October 01, 2005
Bugs!
I have just spent about two hours writing about the second part of favourite logic of september 2005 and, when I saved it as a draft, my firefox just freezed and all the text got erased. Ah well. In view of this and that there is no working computers in my office, I think I will just start posting when I get my powerbook back, which is next week.
Saturday, September 24, 2005
P vs. NP: let's think out loud
We all know this question. It is listed as one of the seven millenium problem by Clay Mathematic Institute. We also know that most people believe that P is different from NP. For example, in the P vs. NP Poll by Gasarch (published in ACM SIGACT Newsletter), out of the 77 people who offered opinion, 61 believed that P is different from NP, 9 believed that P = NP, and others believed that the question is "formally independent" in some form. Well, what do you believe? If you are as yet undecided, I will try to unravel the reasons why most people believe that P is different from NP, and then speak about why it is equally reasonable to believe that P = NP. I will not talk about whether P vs. NP is formally independent of ZFC.
Two most common reasons for believing that P is different from NP are the following:
Well, both of these reasons sound very reasonable. However, I also think that there are holes in these arguments (because of which, it is equally reasonable to believe that P = NP). Most people associate the complexity class P with the set of problems that we can solve "efficiently", and classify non-polynomial algorithms as bad (or inefficient) algorithms. [If you have done some computer science courses, you should see this immediately.] But this is a wrong assumption. For example, the Simplex algorithm for solving linear programming runs in exponential time in the worst case (I believe the same is true in average case), but the algorithm runs very efficiently in practice. There are also polynomial-time algorithms for linear programming, but it seems that none of those have outperformed the simplex algorithm in practice. Furthermore, the exponentiallity of the simplex algorithm's running time only occurs on some pathological examples that never appear in practice. On the other hand, there are many polynomial-time algorithms that do not actually run efficiently in practice. A counterexample for this (quoting Cook's paper) is due to a result by Robertson-Seymour that says that every minor closed family of graphs can be recognized in O(n3), but the hidden constant is so huge that the algorithm is inefficient in practice.
So, maybe there exist polynomial-time algorithms for satisfiability for propositional logic, it's just that the smallest exponents are so big (maybe bigger than the number of atoms in the visible universe, 1090). [Of course, the time hierarchy theorem tells us that there is an problem solvable in nk, but not solvable in nk-1.] Perhaps, the smallest size of the polynomial-time algorithm that solve satisfiability for propositional logic already outnumbers 1090. Who knows! Perhaps, we are good at devising efficient algorithms, but not so good at devising polynomial-time algorithms in general. Maybe the following question is more relevant: assuming that P = NP, give an upper bound on the size of the algorithm (by this I mean, multi-tape Turing Machine) that solves satisfiability in polynomial-time; does it necessarily consist 10, 100, or 1090 states?
In a sense, if you're a practical-minded person, P vs. NP doesn't really matter at all, and there is technical reason why. Recall that the linear speedup theorem (look at Papadimitriou's Computational Complexity) says that if a problem is solvable in `f(n)`, then for any `epsilon > 0`, there exists an algorithm that solves the same problem which runs in `epsilon f(n) + n + 2`. So, if your algorithm runs in 2n, then just use this theorem to speed up your algorithm for all n that is relevant in practice. [Of course, if you check the proof, the size of the resulting algorithm grows quite so quickly in the size of `n`, that there is no way you can write your algorithm on earth. So, the practically-minded people will probably settle with heuristics instead.]
Anyway, I think that it is very possible [correction: 'very' -> 'equally'] that P equals NP, and the proof of which is non-constructive (or we may never actually find the proof, because the length of the shortest possible proofs exceeds the number of atoms in the visible universe).
Two most common reasons for believing that P is different from NP are the following:
- There are (literally) tons of problems which are NP-complete (i.e. if one is in P, and all will be in P), and nobody has been able to devise any polynomial-time algorithm for any of these problems. However, from our experience, we know that we are "good" at devising polynomial-time algorithms, but not very good at proving lower bounds. [Just look at all the great
algorithms we have devised. Also witness that we can't even prove that satisfiability for propositional logic cannot be solved in O(n2).]
- We can intuitively think of P as the set of problems for which we can produce proofs in polynomial time, and of NP as the set of problems for which, given a proof, we can check that it is indeed a proof in polynomial time. Well, from our experience with math, we know that producing proofs is usually much harder than verifying proofs.
Well, both of these reasons sound very reasonable. However, I also think that there are holes in these arguments (because of which, it is equally reasonable to believe that P = NP). Most people associate the complexity class P with the set of problems that we can solve "efficiently", and classify non-polynomial algorithms as bad (or inefficient) algorithms. [If you have done some computer science courses, you should see this immediately.] But this is a wrong assumption. For example, the Simplex algorithm for solving linear programming runs in exponential time in the worst case (I believe the same is true in average case), but the algorithm runs very efficiently in practice. There are also polynomial-time algorithms for linear programming, but it seems that none of those have outperformed the simplex algorithm in practice. Furthermore, the exponentiallity of the simplex algorithm's running time only occurs on some pathological examples that never appear in practice. On the other hand, there are many polynomial-time algorithms that do not actually run efficiently in practice. A counterexample for this (quoting Cook's paper) is due to a result by Robertson-Seymour that says that every minor closed family of graphs can be recognized in O(n3), but the hidden constant is so huge that the algorithm is inefficient in practice.
So, maybe there exist polynomial-time algorithms for satisfiability for propositional logic, it's just that the smallest exponents are so big (maybe bigger than the number of atoms in the visible universe, 1090). [Of course, the time hierarchy theorem tells us that there is an problem solvable in nk, but not solvable in nk-1.] Perhaps, the smallest size of the polynomial-time algorithm that solve satisfiability for propositional logic already outnumbers 1090. Who knows! Perhaps, we are good at devising efficient algorithms, but not so good at devising polynomial-time algorithms in general. Maybe the following question is more relevant: assuming that P = NP, give an upper bound on the size of the algorithm (by this I mean, multi-tape Turing Machine) that solves satisfiability in polynomial-time; does it necessarily consist 10, 100, or 1090 states?
In a sense, if you're a practical-minded person, P vs. NP doesn't really matter at all, and there is technical reason why. Recall that the linear speedup theorem (look at Papadimitriou's Computational Complexity) says that if a problem is solvable in `f(n)`, then for any `epsilon > 0`, there exists an algorithm that solves the same problem which runs in `epsilon f(n) + n + 2`. So, if your algorithm runs in 2n, then just use this theorem to speed up your algorithm for all n that is relevant in practice. [Of course, if you check the proof, the size of the resulting algorithm grows quite so quickly in the size of `n`, that there is no way you can write your algorithm on earth. So, the practically-minded people will probably settle with heuristics instead.]
Anyway, I think that it is very possible [correction: 'very' -> 'equally'] that P equals NP, and the proof of which is non-constructive (or we may never actually find the proof, because the length of the shortest possible proofs exceeds the number of atoms in the visible universe).
Friday, September 23, 2005
Toronto's temperature: the extremes
The last couple of weeks have been quite hot in Toronto (mostly around 25 degrees C). I actually heard that this is unusually hot for September in Toronto. The humidity just makes it worse. You'll find yourself taking a shower three to four times per day.
Since last night, Toronto's temperature has cooled off quite a bit. Throughout today it's been around 18 degree C, just the perfect temperature. I wish it would be like this all year round. But that was just wishful thinking, because I have to be prepared for -20 degrees C in December and January. Actually somebody told me that during winter in Toronto, the wind can be quite strong. This will just make it worse ...
Since last night, Toronto's temperature has cooled off quite a bit. Throughout today it's been around 18 degree C, just the perfect temperature. I wish it would be like this all year round. But that was just wishful thinking, because I have to be prepared for -20 degrees C in December and January. Actually somebody told me that during winter in Toronto, the wind can be quite strong. This will just make it worse ...
Favorite Logic of September 2005: First-order logic (1)
next
Some time ago I promised to make a series of postings on "My Favourite Logic of The Month" every month starting from September 2005. Well, here we officially start until we run out of "nice" logics.
Why first-order logic (FO)? It is the simplest non-trivial logic that we can use to express many mathematical statements. In fact, it is believed that first-order set theory is sufficient to axiomatize mathematics. Besides, most of you have already been exposed to FO, which will make my task much simpler. If any terminologies here sound obscure, check out preliminaries.
We will take a look at three aspects of FO: (1) the problem of testing satisfiability and finite satisfiability, (2) model-checking, and (3) expressive power. I am trying to cover topics that hopefully satisfy finite model theorists, and other logicians. In this posting, I will only speak about (1), saving the other two for some time next week.
Satisfiability: given an FO formula, test whether it is satisfiable. Well, what can we say about this problem with respect to FO? It is undecidable (actually r.e.-complete) [correction: complete for co-r.e, thanks to Richard Zach.]; this is a well-known result proven by Turing, which shattered Hilbert's dream to axiomatize mathematics. If you're into this kind of problem, check out the following book
The Classical Decision Problem by Grädel et al.
Actually, many fragments of FO are decidable, but most are provably intractable. The most complicated such result that I know of is Rabin's result of the decidability of monadic second order theory of infinite binary tree. [Whatever this means, but we may want to delve into this awesome result in the near future.] Although decidable, the problem has non-elementary complexity.
Finite Satisfiability: given an FO formula, test whether it has a finite model. I believe that this problem, if decidable, has more practical applications, e.g., databases. Unfortunately, this problem is also undecidable (actually complete for co-r.e.) [correction: complete for r.e.]. This result is due to Trakhtenbrot. Combining this result and that satisfiability is complete for co-r.e., we can readily imply that completeness theorem, which says that satisfiability is r.e. [correction: satisfiability is co-r.e., thanks to Richard Zach.], fails in the finite. Trakhtenbrot's result in fact marks the beginning of finite model theory. Later on, Fagin proved a logical characterization of NP with a technique that is "isomorphic" to that used to prove Trakhtenbrot's theorem (see this page). For more on finite satisfiability of FO, see Libkin's Elements of Finite Model Theory.
Some time ago I promised to make a series of postings on "My Favourite Logic of The Month" every month starting from September 2005. Well, here we officially start until we run out of "nice" logics.
Why first-order logic (FO)? It is the simplest non-trivial logic that we can use to express many mathematical statements. In fact, it is believed that first-order set theory is sufficient to axiomatize mathematics. Besides, most of you have already been exposed to FO, which will make my task much simpler. If any terminologies here sound obscure, check out preliminaries.
We will take a look at three aspects of FO: (1) the problem of testing satisfiability and finite satisfiability, (2) model-checking, and (3) expressive power. I am trying to cover topics that hopefully satisfy finite model theorists, and other logicians. In this posting, I will only speak about (1), saving the other two for some time next week.
Satisfiability: given an FO formula, test whether it is satisfiable. Well, what can we say about this problem with respect to FO? It is undecidable (actually r.e.-complete) [correction: complete for co-r.e, thanks to Richard Zach.]; this is a well-known result proven by Turing, which shattered Hilbert's dream to axiomatize mathematics. If you're into this kind of problem, check out the following book
The Classical Decision Problem by Grädel et al.
Actually, many fragments of FO are decidable, but most are provably intractable. The most complicated such result that I know of is Rabin's result of the decidability of monadic second order theory of infinite binary tree. [Whatever this means, but we may want to delve into this awesome result in the near future.] Although decidable, the problem has non-elementary complexity.
Finite Satisfiability: given an FO formula, test whether it has a finite model. I believe that this problem, if decidable, has more practical applications, e.g., databases. Unfortunately, this problem is also undecidable (actually complete for co-r.e.) [correction: complete for r.e.]. This result is due to Trakhtenbrot. Combining this result and that satisfiability is complete for co-r.e., we can readily imply that completeness theorem, which says that satisfiability is r.e. [correction: satisfiability is co-r.e., thanks to Richard Zach.], fails in the finite. Trakhtenbrot's result in fact marks the beginning of finite model theory. Later on, Fagin proved a logical characterization of NP with a technique that is "isomorphic" to that used to prove Trakhtenbrot's theorem (see this page). For more on finite satisfiability of FO, see Libkin's Elements of Finite Model Theory.
Thursday, September 08, 2005
CAPTCHA
It stands for Completely Automated Public Turing Test to Tell Computers and Humans Apart. Although I still wonder why it is abbreviated CAPTCHA instead of CAPTTTCHA, it was (re)brought to my attention due to the spam I got for my posting yesterday. Anyway, CAPTCHA is developed by researchers from Carnegie Mellon University. Here is their main website. Briefly, the goal of CAPTCHA project is to use Artificial Intelligence to help internet security (e.g. to prevent spams). The underlying assumption behind CAPTCHA is that there are tasks that humans can do, but computers can't. For example, since I enabled the word verification (from CAPTCHA project), each time you wish leave a comment on this blog, you will be asked to read and verify a distorted text (which is an image file). Although the task seems trivial to humans, tasks like this are non-trivial for computers (at least for now). We don't know whether computers will someday possess our ''intelligence''. But CAPTCHA is one reason why a 'no' answer will have positive impact on our society.
Ironically, the distorted texts are actually generated by computers ...
Ironically, the distorted texts are actually generated by computers ...
Wednesday, September 07, 2005
Back!
Hello all! It's been quite some time since I blogged last. But I am happy to inform you that I can start blogging again on a regular basis.
A little bit about my summer internship in Los Alamos ... I'll start with my work in Los Alamos. I worked mostly on the complexity aspect of Sequential Dynamical Systems (SDS). Briefly, SDSs are a formal model of computer simulation (somewhat like cellular automata) proposed by Los Alamos researchers. I won't tell you more about it (if you are curious as to what they are, read this survey). Anyway, in retrospect Los Alamos was a nice place to visit. The scenery was awesome, the people were friendly, and you can do some cool research there. [Fortunately, what Jon said didn't happen to me or any of my friends.] The down side, however, is that there is pretty much nothing else in Los Alamos. The town is practically dead after 6 --- there is virtually nobody walking on the street. And ... to my surprise, there was no shopping mall whatsoever in Los Alamos. One has to go to Santa Fe, which is the closest biggest city to Los Alamos, to find the nearest shopping mall. Anyway, I will put some pictures from my stay in Los Alamos when I finish developing the pictures.
It is a nice feeling to know that I will be doing logic on a regular basis from this time onwards. I arrived in Toronto last Saturday to start my graduate studies. I haven't completely settled yet, but I couldn't help myself blogging again after the internet connection was set up in my apartment here. Incidentally, this week is Toronto's Computer Science Department's orientation week. I am so happy to meet many logicians here, including some of the most well-known ones. For instance, Moshe Vardi (Rice University) came to visit this Tuesday and gave a talk outlining the development of logic and how computer science was born. I, and I believe most people in the audience (including the non-logicians), found the talk extremely entertaining and insightful. As my advisor, Leonid Libkin, put it this morning, Vardi has the rare gift to be both a top-notch researcher and an excellent speaker. [As you and I know, most researchers who do great research are poor at explaining their research to others.]
Anyhow, that is all I have for now. As a final remark, I haven't forgotten about my favourite logic of the month and will write on it some time next week after I have completely settled.
A little bit about my summer internship in Los Alamos ... I'll start with my work in Los Alamos. I worked mostly on the complexity aspect of Sequential Dynamical Systems (SDS). Briefly, SDSs are a formal model of computer simulation (somewhat like cellular automata) proposed by Los Alamos researchers. I won't tell you more about it (if you are curious as to what they are, read this survey). Anyway, in retrospect Los Alamos was a nice place to visit. The scenery was awesome, the people were friendly, and you can do some cool research there. [Fortunately, what Jon said didn't happen to me or any of my friends.] The down side, however, is that there is pretty much nothing else in Los Alamos. The town is practically dead after 6 --- there is virtually nobody walking on the street. And ... to my surprise, there was no shopping mall whatsoever in Los Alamos. One has to go to Santa Fe, which is the closest biggest city to Los Alamos, to find the nearest shopping mall. Anyway, I will put some pictures from my stay in Los Alamos when I finish developing the pictures.
It is a nice feeling to know that I will be doing logic on a regular basis from this time onwards. I arrived in Toronto last Saturday to start my graduate studies. I haven't completely settled yet, but I couldn't help myself blogging again after the internet connection was set up in my apartment here. Incidentally, this week is Toronto's Computer Science Department's orientation week. I am so happy to meet many logicians here, including some of the most well-known ones. For instance, Moshe Vardi (Rice University) came to visit this Tuesday and gave a talk outlining the development of logic and how computer science was born. I, and I believe most people in the audience (including the non-logicians), found the talk extremely entertaining and insightful. As my advisor, Leonid Libkin, put it this morning, Vardi has the rare gift to be both a top-notch researcher and an excellent speaker. [As you and I know, most researchers who do great research are poor at explaining their research to others.]
Anyhow, that is all I have for now. As a final remark, I haven't forgotten about my favourite logic of the month and will write on it some time next week after I have completely settled.
Tuesday, June 07, 2005
Interning in Los Alamos National Laboratory
Howdy! I have just recently started a summer research internship in Los Alamos National Laboratory. As my summer research topic is not directly related to logic, I will probably have to switch to a hibernation mode as far as blogging Logicomp is concerned. I will definitely resume with Logicomp when I start my graduate studies in Toronto (early September). One interesting thing that I plan to post on Logicomp in the future is the "Favorite Logic of the Month" in which I will mention my favorite logic of that month and a general method for proving (in)expressibility.
Anyway, until then I hope everyone have a great time!
Anyway, until then I hope everyone have a great time!
Monday, May 30, 2005
Nice finite model theory course notes
I have recently found nice introductory course notes on finite model theory. You can find it here. Thanks to the author for making the notes publicly available.
Sunday, May 29, 2005
No compactness in finite model theory
The compactness theorem for first-order logic is indisputably the most fundamental theorem in model theory. It says that
A theory has a model iff every finite subset of it has a model
I will say no more about the usefulness of this theorem in model theory. But what I will speak about now is the failure of compactness in finite model theory, as I already remarked before.
In finite model theory (FMT), we are only concerned with finite structures. Hence compactness theorem in FMT would read
A theory has a finite model iff every subset of it has a finite model
It is easy to conjure a counterexample for this statement. Consider the first-order theory `T` over the empty vocabulary containing sentences of the following form (for all `k >= 2`):
`S_k = EE x_1,...,x_k( x_1 != x_2 ^^ x_1 != x_3 ^^ cdots ^^ x_{k-1} != x_k )`
It is easy to see that every subset `T'` of `T` has a finite model; if `n` is the largest integer such that `S_n in T'`, then the structure containing `n` elements satisfies `T'`. It is also easy to see that `T` has no finite model. (QED)
Likewise, many other fundamental theorems in model theory, such as Craig Interpolation Theorem, are also casualties of finitization (more on this later); Ehrenfeucht-Fraisse games being the only general tool available for proving inexpressibility results in finite model theory.
A theory has a model iff every finite subset of it has a model
I will say no more about the usefulness of this theorem in model theory. But what I will speak about now is the failure of compactness in finite model theory, as I already remarked before.
In finite model theory (FMT), we are only concerned with finite structures. Hence compactness theorem in FMT would read
A theory has a finite model iff every subset of it has a finite model
It is easy to conjure a counterexample for this statement. Consider the first-order theory `T` over the empty vocabulary containing sentences of the following form (for all `k >= 2`):
`S_k = EE x_1,...,x_k( x_1 != x_2 ^^ x_1 != x_3 ^^ cdots ^^ x_{k-1} != x_k )`
It is easy to see that every subset `T'` of `T` has a finite model; if `n` is the largest integer such that `S_n in T'`, then the structure containing `n` elements satisfies `T'`. It is also easy to see that `T` has no finite model. (QED)
Likewise, many other fundamental theorems in model theory, such as Craig Interpolation Theorem, are also casualties of finitization (more on this later); Ehrenfeucht-Fraisse games being the only general tool available for proving inexpressibility results in finite model theory.
Saturday, May 28, 2005
Finite Model Theory: Preliminaries (2)
We now focus on a very important concept in finite model theory: `k`-ary queries. In fact, one goal of finite model theory is to establish a useful, if possible complete, criterion for determining expressibility (ie, definability) of a query in a logic (such as, first-order logic) on finite structures. For example, we may ask if the query connectivity for finite graphs, which asks whether a finite graph is connected, is expressible in first-order logic. The answer is 'no', though we won't prove this now. [Curious readers are referred to Libkin's Elements of Finite Model Theory or Fagin's excellent survey paper.]
We shall start by recalling the notion of homomorphisms and isomorphisms between structures. Given two `sigma`-structures `fr A` and `fr B`, a homomorphism between them is a function `h: A -> B` such that `h(c^{fr A}) = c^{fr B}` for every constant symbol `c in sigma`, and `h(bb a) := (h(a_1), ..., h(a_r)) in R^{fr B}`, for every `r`-ary relation symbol `R in sigma` and `bb a := (a_1,...,a_r) in R^{fr A}`. So, homomorphisms are tuple-preserving functions (here, think of a tuple as an `r`-ary vector prepended by an `r`-ary relation symbol, eg, `R(1,2,3)`). Now isomorphisms are basically bijective homomorphisms whose inverse are also homomorphisms. Intuitively, this means that two isomorphic structures are the same after relabeling the elements of the universe in one of these structures. We write `fr A ~= fr B` to denote that `fr A` and `fr B` be isomorphic.
Now we define what we mean by queries. Fix a vocabulary `sigma` and a class `cc M` of (not necessarily all) finite `sigma`-structures. This class `cc M` will be referred to as a ground set. Now, for `k >= 0`, a `k`-ary query `cc Q` is a function associating each `fr A in cc M` to a subset of `A^k` such that `cc Q` is closed under isomorphisms, ie, whenever `h: A -> B` is an isomorphism, we have `h( cc Q(fr A)) = cc Q(fr B)`. Now this query `cc Q` is said to be expressible (or definable) in a logic `L` over `cc M` if there exists a `L`-formula `phi` over `sigma` with `k` free variables such that for every `fr A in cc M`, `cc Q(fr A) = phi(fr A)` where
`phi(fr A) := { (a_1,...,a_k) in A^k : fr A |= phi(a_1,...,a_k) }`.
Whenever `cc M` be the set of all finite structures, we shall omit mention of `cc M`.
An important special case occurs when `k = 0`. Such queries are normally called boolean queries or just properties. In this case, the image of `cc Q` can only be either a singleton `{()}` containing the trivial tuple `()`, or the empty set `O/`. We will identify `{()}` with `true` and `O/` with `false`. So, a property `cc Q` is expressible in a logic `L` over `cc M` if there exists an `L`-sentence `phi` over `sigma` such that `cc Q(fr A) = true` iff `fr A |= phi`, for each `fr A in cc M`. Examples of boolean queries (for finite graphs) are:
An example of 2-ary queries is the transitive closure query of finite graphs:
`Q: fr G |-> { (a,b) in G^2 : text{there exists a path from } a text{ to } b text{ in} fr G }`
Question: which of the above queries are expressible in first-order logic? Well, we already saw that Self-loop is expressible in first-order logic. So, it is enough to exhibit a first-order formula to show that a query be expressible in first-order logic. But how do we prove first-order inexpressibility results? In classical model theory, we have tools like compactness and Lowenheim-Skolem theorems for proving first-order inexpressibility. However, most of these tools including the two afore-mentioned theorems fail to "work" in the finite. The only one result that survives is the Ehrenfeucht-Fraisse games (a good exposition of the result can be found here). [Incidentally, does this imply that finite model theory is more difficult than classical model theory?] The games, for example, can be used to prove that the queries Hamiltonian, Connected, Acyclic, and Transitive Closure are not definable in first-order logic. These results will be discussed in subsequent postings.
We shall start by recalling the notion of homomorphisms and isomorphisms between structures. Given two `sigma`-structures `fr A` and `fr B`, a homomorphism between them is a function `h: A -> B` such that `h(c^{fr A}) = c^{fr B}` for every constant symbol `c in sigma`, and `h(bb a) := (h(a_1), ..., h(a_r)) in R^{fr B}`, for every `r`-ary relation symbol `R in sigma` and `bb a := (a_1,...,a_r) in R^{fr A}`. So, homomorphisms are tuple-preserving functions (here, think of a tuple as an `r`-ary vector prepended by an `r`-ary relation symbol, eg, `R(1,2,3)`). Now isomorphisms are basically bijective homomorphisms whose inverse are also homomorphisms. Intuitively, this means that two isomorphic structures are the same after relabeling the elements of the universe in one of these structures. We write `fr A ~= fr B` to denote that `fr A` and `fr B` be isomorphic.
Now we define what we mean by queries. Fix a vocabulary `sigma` and a class `cc M` of (not necessarily all) finite `sigma`-structures. This class `cc M` will be referred to as a ground set. Now, for `k >= 0`, a `k`-ary query `cc Q` is a function associating each `fr A in cc M` to a subset of `A^k` such that `cc Q` is closed under isomorphisms, ie, whenever `h: A -> B` is an isomorphism, we have `h( cc Q(fr A)) = cc Q(fr B)`. Now this query `cc Q` is said to be expressible (or definable) in a logic `L` over `cc M` if there exists a `L`-formula `phi` over `sigma` with `k` free variables such that for every `fr A in cc M`, `cc Q(fr A) = phi(fr A)` where
`phi(fr A) := { (a_1,...,a_k) in A^k : fr A |= phi(a_1,...,a_k) }`.
Whenever `cc M` be the set of all finite structures, we shall omit mention of `cc M`.
An important special case occurs when `k = 0`. Such queries are normally called boolean queries or just properties. In this case, the image of `cc Q` can only be either a singleton `{()}` containing the trivial tuple `()`, or the empty set `O/`. We will identify `{()}` with `true` and `O/` with `false`. So, a property `cc Q` is expressible in a logic `L` over `cc M` if there exists an `L`-sentence `phi` over `sigma` such that `cc Q(fr A) = true` iff `fr A |= phi`, for each `fr A in cc M`. Examples of boolean queries (for finite graphs) are:
- Hamiltonian: `cc Q(fr G) = true` iff the graph `fr G` is hamiltonian.
- Self-loop: `cc Q(fr G) = true` iff the graph `fr G` has a self-loop (ie, `fr G |= EE x( E(x,x))`).
- Isolated: `cc Q(fr G) = true` iff the graph `fr G` has an isolated vertex.
- Connected: `cc Q(fr G) = true` iff the graph `fr G` is connected.
- Acyclic: `cc Q(fr G) = true` iff the graph `fr G` is acyclic.
An example of 2-ary queries is the transitive closure query of finite graphs:
`Q: fr G |-> { (a,b) in G^2 : text{there exists a path from } a text{ to } b text{ in} fr G }`
Question: which of the above queries are expressible in first-order logic? Well, we already saw that Self-loop is expressible in first-order logic. So, it is enough to exhibit a first-order formula to show that a query be expressible in first-order logic. But how do we prove first-order inexpressibility results? In classical model theory, we have tools like compactness and Lowenheim-Skolem theorems for proving first-order inexpressibility. However, most of these tools including the two afore-mentioned theorems fail to "work" in the finite. The only one result that survives is the Ehrenfeucht-Fraisse games (a good exposition of the result can be found here). [Incidentally, does this imply that finite model theory is more difficult than classical model theory?] The games, for example, can be used to prove that the queries Hamiltonian, Connected, Acyclic, and Transitive Closure are not definable in first-order logic. These results will be discussed in subsequent postings.
Friday, May 27, 2005
Finite Model Theory: Preliminaries (1)
I realize that in the previous postings I haven't been as precise as I can possibly be. It's all about to change: we shall now fix terminologies for our subsequent discussion on finite model theory. We will however have to divide this "section" into two postings, as it is too long for one. We shall also assume that the reader knows basic facts from mathematical logic (see Enderton's A Mathematical Introduction To Logic).
We can start by discussing what finite model theory is. One common definition for finite model theory is the model theory of finite structures. Precise, but perhaps too succinct. What makes it different from classical model theory? Finite model theory is primarily concerned with finite structures, while model theory with both finite and infinite structures. Hence, one can expect that the definitions used in finite model theory are very similar to those in classical model theory. The restriction to finite structures is necessary for studying computers and computation due to their finite nature. Note also that finiteness doesn't necessarily imply triviality. For example, witness that (finite) graph theory is a deep, rich, and beautiful subject, which has captivated brilliant mathematicians from many generations including Euler and Erdos.
Unless otherwise stated, we shall make the following assumptions in subsequent postings on finite model theory:
I am going to adopt an extremely useful definition of expansion of structures from Libkin's Elements of Finite Model Theory, which will allow us to convert back and forth between formulas and sentences. Let `fr A` and `fr A'` be structures over, respectively, `sigma` and `sigma'` where `sigma nn sigma' = O/`. The expansion of `fr A` by `fr A'`, denoted by `(fr A,fr A')`, is the `sigma uu sigma'`-structure with all symbols from `sigma` interpreted according to `fr A`, and from `sigma'` interpreted according to `fr A'`. An important special case is when `sigma'` be the vocabulary `sigma_n` containing only constant symbols `c_1,cdots,c_n`. In this case, if `fr A' = (a_1, cdots, a_n)` (with `a_i` interpreting `c_i`), we can omit some redundant brackets and write `(fr A, fr A') = (fr A, a_1, cdots, a_n)`. We have the following lemma:
Lemma: Suppose `phi(x_1, cdots, x_n)` be a `sigma`-formula, and `fr A` be a `sigma`-structure. Let `Phi` be the formula `phi(c_1/x_1,cdots,c_n/x_n)`, ie, each occurence of `x_i` is replaced by a brand new constant symbol `c_i`. Then, we have: `fr A |= phi(a_1,cdots,a_n)` iff `(fr A,a_1,cdots,a_n) |= Phi`.
Finally, we need to define the notion of `k`-ary queries, which we will do in the next posting.
We can start by discussing what finite model theory is. One common definition for finite model theory is the model theory of finite structures. Precise, but perhaps too succinct. What makes it different from classical model theory? Finite model theory is primarily concerned with finite structures, while model theory with both finite and infinite structures. Hence, one can expect that the definitions used in finite model theory are very similar to those in classical model theory. The restriction to finite structures is necessary for studying computers and computation due to their finite nature. Note also that finiteness doesn't necessarily imply triviality. For example, witness that (finite) graph theory is a deep, rich, and beautiful subject, which has captivated brilliant mathematicians from many generations including Euler and Erdos.
Unless otherwise stated, we shall make the following assumptions in subsequent postings on finite model theory:
- Every vocabulary and structure is relational, ie, has no function symbols and functions.
- Every vocabulary has finitely many (constant and relation) symbols.
- Capital Fraktur fonts are used to denote structures; their corresponding letters in Latin correspond to their universes. For example, a structure `fr A` has universe `A`.
I am going to adopt an extremely useful definition of expansion of structures from Libkin's Elements of Finite Model Theory, which will allow us to convert back and forth between formulas and sentences. Let `fr A` and `fr A'` be structures over, respectively, `sigma` and `sigma'` where `sigma nn sigma' = O/`. The expansion of `fr A` by `fr A'`, denoted by `(fr A,fr A')`, is the `sigma uu sigma'`-structure with all symbols from `sigma` interpreted according to `fr A`, and from `sigma'` interpreted according to `fr A'`. An important special case is when `sigma'` be the vocabulary `sigma_n` containing only constant symbols `c_1,cdots,c_n`. In this case, if `fr A' = (a_1, cdots, a_n)` (with `a_i` interpreting `c_i`), we can omit some redundant brackets and write `(fr A, fr A') = (fr A, a_1, cdots, a_n)`. We have the following lemma:
Lemma: Suppose `phi(x_1, cdots, x_n)` be a `sigma`-formula, and `fr A` be a `sigma`-structure. Let `Phi` be the formula `phi(c_1/x_1,cdots,c_n/x_n)`, ie, each occurence of `x_i` is replaced by a brand new constant symbol `c_i`. Then, we have: `fr A |= phi(a_1,cdots,a_n)` iff `(fr A,a_1,cdots,a_n) |= Phi`.
Finally, we need to define the notion of `k`-ary queries, which we will do in the next posting.
Monday, May 23, 2005
The Unusual Effectiveness of Logic in Computer Science
A couple of days ago I found a non-technical logic-in-computer-science paper in my folder of unused papers that has turned out to be a highly interesting read. The paper is:
On the Unusual Effectiveness of Logic in Computer Science by Halpern, Halper, Immerman, Kolaitis, Vardi, and Vianu
The authors of these papers are well-renowned authorities in the area of logic in computer science, each with his own enormous contribution to the area.
Here is a summary of the paper. The authors start by mentioning two attempts of explaning the unreasonable effectiveness of mathematics in natural sciences by E.P. Wigner, a Nobel Laureate for Physics, and R.W. Hamming, an ACM Turing Award (which can be construed as the Nobel Prize for Computer Science) winner. In their separate papers, Wigner and Hamming give a number of examples supporting his argument, but conclude that the question "Why is mathematics so unreasonably effective" remains open. The above paper by Halpern et al. is basically an attempt to answer the question "why logic is so effective in computer science". Like Wigner and Hamming did, Halpern et al. give a number of examples supporting their assertion:
Aside: I would love to see proof complexity and bounded arithemetic discussed in this paper.
Incidentally, Halpern et al. make a very interesting remark in their paper --- that logic seems more connected to computer science than to mathematics. To a theoretical computer scientist like myself, this claim is so conspicuous. I'm curious whether philosophers and/or mathematicians and/or logicians think so too ...
On the Unusual Effectiveness of Logic in Computer Science by Halpern, Halper, Immerman, Kolaitis, Vardi, and Vianu
The authors of these papers are well-renowned authorities in the area of logic in computer science, each with his own enormous contribution to the area.
Here is a summary of the paper. The authors start by mentioning two attempts of explaning the unreasonable effectiveness of mathematics in natural sciences by E.P. Wigner, a Nobel Laureate for Physics, and R.W. Hamming, an ACM Turing Award (which can be construed as the Nobel Prize for Computer Science) winner. In their separate papers, Wigner and Hamming give a number of examples supporting his argument, but conclude that the question "Why is mathematics so unreasonably effective" remains open. The above paper by Halpern et al. is basically an attempt to answer the question "why logic is so effective in computer science". Like Wigner and Hamming did, Halpern et al. give a number of examples supporting their assertion:
- Example 1: Descriptive Complexity. The reader should know roughly what this is by now.
- Example 2: Logic as a Database Query Language. This area is devoted to the study of abstract query languages in database theory. Examples of abstract query languages are relational calculus (equivalent to first-order logic), and conjunctive queries (see here for a definition).
- Example 3: Type Theory in Programming Language Research. Type theory is often used for building useful type systems for strongly-typed programming languages including Haskell (the computer science reader should know that C, for example, is not strongly-typed).
- Example 4: Reasoning about Knowledge. You may think of this area as "the theory of agents". Reasoning about knowledge plays a key role in burgeoning computer science fields including distributed computing, game theory, and AI.
- Example 5: Automated Verification in Semiconductor Designs. The meaning is self-explanatory.
Aside: I would love to see proof complexity and bounded arithemetic discussed in this paper.
Incidentally, Halpern et al. make a very interesting remark in their paper --- that logic seems more connected to computer science than to mathematics. To a theoretical computer scientist like myself, this claim is so conspicuous. I'm curious whether philosophers and/or mathematicians and/or logicians think so too ...
Friday, May 20, 2005
MathML
Recently I said that a good logic blogger needs to learn something like MathML. Well ... I have just taken a first step in this direction: enable the MathML mode on this website.
Also, I have just recently found ASCIIMathML, thanks to a posting in Andrej Bauer's blog. This script allows you to write math formulas in a LaTeX-like notation. This takes away the burden of learning MathML.
If your browser cannot display MathML, then here is a suggestion (look at 'system requirements' section).
Also, I have just recently found ASCIIMathML, thanks to a posting in Andrej Bauer's blog. This script allows you to write math formulas in a LaTeX-like notation. This takes away the burden of learning MathML.
If your browser cannot display MathML, then here is a suggestion (look at 'system requirements' section).
What the tortoise said to achilles
Howdy! Today I am pleased to learn that somebody is actually reading my blog and has left some useful and encouraging comments. Thanks to all who have participated.
One of the good comments I received was a reference to What The Tortoise Said to Achilles by Lewis Carrol, in response to my question in the previous posting whether logicians have a sense of humor. Incidentally, my hunch says I've seen this article in Douglas Hofstadter's excellent Godel, Escher, Bach: An Eternal Golden Braid.
Anyway, on with the story. Basically, Carrol's article contains a clever and well-constructed argument that reasoning is impossible without using an infinite series of modus ponens. I personally feel this argument itself already shows that logicians are humorous (well ... more precisely, logically humorous). I leave the reader to ponder whether Carrol's article shows that logicians have a sense of humor.
Oh, incidentally, I was quite surprised to learn the well-renowned 'Alice's Adventures in Wonderland' is also written by Lewis Carrol, a logician. Wow!
One of the good comments I received was a reference to What The Tortoise Said to Achilles by Lewis Carrol, in response to my question in the previous posting whether logicians have a sense of humor. Incidentally, my hunch says I've seen this article in Douglas Hofstadter's excellent Godel, Escher, Bach: An Eternal Golden Braid.
Anyway, on with the story. Basically, Carrol's article contains a clever and well-constructed argument that reasoning is impossible without using an infinite series of modus ponens. I personally feel this argument itself already shows that logicians are humorous (well ... more precisely, logically humorous). I leave the reader to ponder whether Carrol's article shows that logicians have a sense of humor.
Oh, incidentally, I was quite surprised to learn the well-renowned 'Alice's Adventures in Wonderland' is also written by Lewis Carrol, a logician. Wow!
Wednesday, May 18, 2005
How to be a good blogger
Having just started my own blog, I have recently been thinking about what one needs to do to be a good math/logic blogger. After some serious meditations, I realize that this question is equivalent to 'how to make a fine piece of math/logic writing', whose answers can be found in books like Mathematical Writing by Donald Knuth et al. Nevertheless, there are some additional, but equally important, things that good bloggers need to do:
I guess I have hitherto successfully and continuously violated every single one of these tips (Oops). Ah well ... I guess there is still tomorrow.
- Be controversial.
- Utilize the ability to hyperlink (preferrably to free online resources).
- Learn how to use MathML. Here is a seemingly good
tutorial (I haven't perused this meticulously enough though). If you already know LaTeX and are using a Unix-like OS, you may want to use Ttm to convert LaTeX to MathML.
- Lastly, having just a bit of sense of humor doesn't hurt. I wonder though if logicians have a sense of humor?
I guess I have hitherto successfully and continuously violated every single one of these tips (Oops). Ah well ... I guess there is still tomorrow.
Tuesday, May 17, 2005
Unary-conjunctive-view Query Language (1)
Last December I completed my BSc(Honours) degree, the Australian equivalent of American BSc degree, at the University of Melbourne (Australia). So, before I am leaving for North America for graduate studies, I thought it might be a good idea to write something about the finite-model-theory related problem I worked on for my undergraduate thesis. It might also be a good topic to get this blog started.
The story is somewhat lengthy. So, I will divide it into a series of bite-size chunks.
To get under way, recall that pure first-order logic is undecidable. [When we say that a logic is (un)decidable, we mean that its satisfiability problem is (un)decidable.] Here pure first-order logic basically consists of all first-order sentences without equality and function symbols. Turing proved this by reducing the halting problem for Turing machines to deciding the satisfiability of first-order logic. We know on the other hand that pure monadic first-order logic (MFO) is decidable, actually complete for NEXPTIME. Here the term 'monadic' simply means that the relation symbols in each formula in MFO are of arity 1. This decidability result actually lies at the border of the decidable and the undecidable because permitting merely one binary relation symbol to MFO immediately results in undecidability.
So, the question boils down to how much more can we extend MFO before we get an undecidable logic? Strictly speaking, this is not really a mathematical question, and so has no single correct answer. I'll mention three known successful attempts to extend the decidability of MFO:
All of these results are optimum. For example, adding one more function symbol to the third logic in this list results in undecidability. For more information on these logics, the reader is referred to the reference book for the classical decision problem. We will however explore a different avenue to answer this question.
Database theorists often talk about conjunctive queries: pure first-order formulas that can be written as
where the x's are the free variables, the y's are the bound variables, and the u's are tuples of variables appropriate for the (arities of the) R's. Following notations from logic programming, we will write the formula F as
The set of all these F's forms the conjunctive query language. Now, it is easy to see that any conjunctive query is satisfiable --- so its satisfiability problem is trivial. Here is the twist. We can combine MFO and a restricted version of conjunctive query language to make a decidable logic.
Let U be the set of all conjunctive queries with exactly one free variable (a.k.a. unary conjunctive queries). We call U a view vocabulary (signature). Let UCV be the smallest set that satisfies the following conditions:
The Unary-Conjunctive-View query language is the logic UCV. To get a feel for UCV, let us start speaking in it. For example, this logic can assert the following graph-theoretic sentence "any vertex has a 4-walk but no self-loop". How? Consider the following two conjunctive queries:
Then, the desired sentence is $AA x ( text{CW_4}(x) ^^ not text{Loop}(x) )$. We can readily see that this logic is quite expressive as it permits any number of relation symbols of any arity. This also shows that UCV is strictly more expressive than MFO and the conjunctive query language, considered individually. Nonetheless, the logic is much less expressive than the first-order logic. For example, UCV cannot even assert simple query like "there exists a path (ie, walks where none of the vertices are visited twice) of length k", for any fixed k > 0. [We'll prove this later.]
In the next posting, I will sketch a proof that UCV is decidable, actually solvable in 2-NEXPTIME but is NEXPTIME-hard. Our proof taps into the fact that UCV has the bounded model property, i.e., every satisfiable query Q in UCV has a model of size at most f(|Q|) for some computable function f:N->N where |Q| denotes the size of the encoding of Q. Note that bounded model property immediately implies decidability in SPACE(f(|Q|)), assuming that f is a proper complexity function, as a Turing machine can start by computing f(|Q|), enumerate every possible structure A appropriate for Q one-by-one, and for each A test whether A satisfies Q (which can be also be done in SPACE(f(|Q|)) ).
Later on we will explore the expressive power of UCV and a general method for proving inexpressibility in UCV.
The story is somewhat lengthy. So, I will divide it into a series of bite-size chunks.
To get under way, recall that pure first-order logic is undecidable. [When we say that a logic is (un)decidable, we mean that its satisfiability problem is (un)decidable.] Here pure first-order logic basically consists of all first-order sentences without equality and function symbols. Turing proved this by reducing the halting problem for Turing machines to deciding the satisfiability of first-order logic. We know on the other hand that pure monadic first-order logic (MFO) is decidable, actually complete for NEXPTIME. Here the term 'monadic' simply means that the relation symbols in each formula in MFO are of arity 1. This decidability result actually lies at the border of the decidable and the undecidable because permitting merely one binary relation symbol to MFO immediately results in undecidability.
So, the question boils down to how much more can we extend MFO before we get an undecidable logic? Strictly speaking, this is not really a mathematical question, and so has no single correct answer. I'll mention three known successful attempts to extend the decidability of MFO:
- MFO with equality. Lowenheim, who proved the decidability of MFO, proved this too.
- MFO with any number of function symbols. This is Lob-Gurevich theorem.
- MFO with equality and one function symbol. This is proved by Rabin in one of his groundbreaking papers.
All of these results are optimum. For example, adding one more function symbol to the third logic in this list results in undecidability. For more information on these logics, the reader is referred to the reference book for the classical decision problem. We will however explore a different avenue to answer this question.
Database theorists often talk about conjunctive queries: pure first-order formulas that can be written as
where the x's are the free variables, the y's are the bound variables, and the u's are tuples of variables appropriate for the (arities of the) R's. Following notations from logic programming, we will write the formula F as
The set of all these F's forms the conjunctive query language. Now, it is easy to see that any conjunctive query is satisfiable --- so its satisfiability problem is trivial. Here is the twist. We can combine MFO and a restricted version of conjunctive query language to make a decidable logic.
Let U be the set of all conjunctive queries with exactly one free variable (a.k.a. unary conjunctive queries). We call U a view vocabulary (signature). Let UCV be the smallest set that satisfies the following conditions:
- U is a subset of UCV.
- UCV is closed under boolean operations and first-order quantifications.
The Unary-Conjunctive-View query language is the logic UCV. To get a feel for UCV, let us start speaking in it. For example, this logic can assert the following graph-theoretic sentence "any vertex has a 4-walk but no self-loop". How? Consider the following two conjunctive queries:
Then, the desired sentence is $AA x ( text{CW_4}(x) ^^ not text{Loop}(x) )$. We can readily see that this logic is quite expressive as it permits any number of relation symbols of any arity. This also shows that UCV is strictly more expressive than MFO and the conjunctive query language, considered individually. Nonetheless, the logic is much less expressive than the first-order logic. For example, UCV cannot even assert simple query like "there exists a path (ie, walks where none of the vertices are visited twice) of length k", for any fixed k > 0. [We'll prove this later.]
In the next posting, I will sketch a proof that UCV is decidable, actually solvable in 2-NEXPTIME but is NEXPTIME-hard. Our proof taps into the fact that UCV has the bounded model property, i.e., every satisfiable query Q in UCV has a model of size at most f(|Q|) for some computable function f:N->N where |Q| denotes the size of the encoding of Q. Note that bounded model property immediately implies decidability in SPACE(f(|Q|)), assuming that f is a proper complexity function, as a Turing machine can start by computing f(|Q|), enumerate every possible structure A appropriate for Q one-by-one, and for each A test whether A satisfies Q (which can be also be done in SPACE(f(|Q|)) ).
Later on we will explore the expressive power of UCV and a general method for proving inexpressibility in UCV.
Monday, May 16, 2005
Welcome to Logicomp!
Hello all! Throughout the past two years, I have learned a lot from Lance Fortnow's successful complexity blog. Professor Fortnow has been an excellent blogger, and kept his avid readers informed on the lattest and the must-know about complexity theory. His blog was certainly one of the things that got me interested in complexity theory, and will continue inspiring me in the future.
Although Professor Fortnow's blog covers many topics in complexity theory, it is a pity that the blog rarely touches on the elegant connection between logic and complexity theory, which --- God knows why --- many finite model theorists think will be a key to proving that P does not equal NP. For example, here are some deep results in the area:
So, in order to prove that P does not equal NP, it suffices to prove that the set of properties of finite structures expressible in ESO is different from that expressible in ASO. In fact, to prove this it is enough to show that the property 3-colorability is not expressible in ASO on the class of finite graphs. That is, we have reduced an important problem in complexity theory to a problem in finite model theory. The area of theoretical computer science that explores the connection between finite model theory and complexity theory is called descriptive complexity.
In view of these, I thought it would be a good idea for me to start a blog that aims to explore the deep connection between logic and complexity. Nonetheless, I realize that it is a formidable task to be a good blogger even for a small subarea of logic and complexity, especially for a newbie like myself. Thus, I will try to focus on areas that I will explore during my graduate studies: (finite and infinite) model theory and descriptive complexity, proof complexity, and perhaps bounded arithmetic. [Nonetheless, I will probably have to every now and then violate this rule and speak about other things that I find interesting and fun.] So, from now on, when I speak about 'Logic and Complexity', I will be referring to these subareas. There are already excellent blogs that cover logic, like this one maintained by Professor Restall at The University of Melbourne's Department of Philosophy, and logic and computation, like this one. However, none of these cover the stuff that I plan to talk about here such as finite model theory and descriptive complexity.
Anyway, for a starter, I plan to write a concise introduction to finite model theory that other mathematical readers, who know a bit of logic, can read. I will try to post this bit-by-bit every week. Any other ideas? Feel free to comment.
Although Professor Fortnow's blog covers many topics in complexity theory, it is a pity that the blog rarely touches on the elegant connection between logic and complexity theory, which --- God knows why --- many finite model theorists think will be a key to proving that P does not equal NP. For example, here are some deep results in the area:
- Fagin's theorem: the set of properties of (relational) finite structures expressible in existential second-order logic (ESO) coincides with NP.
- Dual Fagin's theorem: the set of properties of finite structures expressible in universal second-order logic (ASO) coincides with co-NP.
- The set of properties of finite structures expressible in second-order logic (SO) coincides with PH.
So, in order to prove that P does not equal NP, it suffices to prove that the set of properties of finite structures expressible in ESO is different from that expressible in ASO. In fact, to prove this it is enough to show that the property 3-colorability is not expressible in ASO on the class of finite graphs. That is, we have reduced an important problem in complexity theory to a problem in finite model theory. The area of theoretical computer science that explores the connection between finite model theory and complexity theory is called descriptive complexity.
In view of these, I thought it would be a good idea for me to start a blog that aims to explore the deep connection between logic and complexity. Nonetheless, I realize that it is a formidable task to be a good blogger even for a small subarea of logic and complexity, especially for a newbie like myself. Thus, I will try to focus on areas that I will explore during my graduate studies: (finite and infinite) model theory and descriptive complexity, proof complexity, and perhaps bounded arithmetic. [Nonetheless, I will probably have to every now and then violate this rule and speak about other things that I find interesting and fun.] So, from now on, when I speak about 'Logic and Complexity', I will be referring to these subareas. There are already excellent blogs that cover logic, like this one maintained by Professor Restall at The University of Melbourne's Department of Philosophy, and logic and computation, like this one. However, none of these cover the stuff that I plan to talk about here such as finite model theory and descriptive complexity.
Anyway, for a starter, I plan to write a concise introduction to finite model theory that other mathematical readers, who know a bit of logic, can read. I will try to post this bit-by-bit every week. Any other ideas? Feel free to comment.
Subscribe to:
Comments (Atom)